
已知函數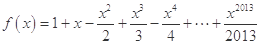 設
設 ,且函數F(x)的零點均在區間
,且函數F(x)的零點均在區間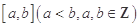 內,圓
內,圓 的面積的最小值是 ( )
的面積的最小值是 ( )
A.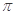 B.
B.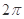 C.
C. D.
D.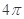
 華東師大版一課一練系列答案
華東師大版一課一練系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中數學 來源: 題型:
| k |
| x |
| 1 |
| e |
| 1 |
| e |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2011 |
| 2011 |
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2011 |
| 2011 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源:浙江省新安江中學2012屆高三10月月考數學理科試題 題型:044
已知函數f(x)=ax2+bx+1(a,b為實數,a≠0,x∈R),F(x)=![]()
(1)若f(-1)=0,且函數f(x)的值域為[0,+∞),求F(x)的表達式;
(2)在(1)的條件下,當x∈[-2,2]時,g(x)=f(x)-kx是單調函數,求實數k的取值范圍;
(3)設mn<0,m+n>0,a>0,且函數f(x)為偶函數,判斷F(m)+F(n)是否大于0?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com