
如圖,海上有 兩個小島相距10
兩個小島相距10 ,船O將保持觀望A島和B島所成的視角為
,船O將保持觀望A島和B島所成的視角為 ,現從船O上派下一只小艇沿
,現從船O上派下一只小艇沿 方向駛至
方向駛至 處進行作業,且
處進行作業,且 .設
.設
 。
。
(1)用 分別表示
分別表示 和
和 ,并求出
,并求出 的取值范圍;
的取值范圍;
(2)晚上小艇在 處發出一道強烈的光線照射A島,B島至光線
處發出一道強烈的光線照射A島,B島至光線 的距離為
的距離為 ,求BD的最大值.
,求BD的最大值.
(1)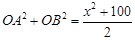 ;
;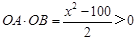 ,
,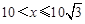 (2)
(2)
解析試題分析:(1)在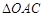 和
和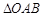 中,分別用余弦定理AC,AB,然后兩式相加即得
中,分別用余弦定理AC,AB,然后兩式相加即得 的表達式;兩式相減即得
的表達式;兩式相減即得 的表達式,由
的表達式,由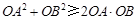 和
和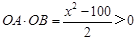 確定x的取值范圍.(2)由
確定x的取值范圍.(2)由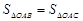 、
、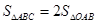 和
和
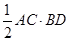 可得到關于BD的函數式,然后通過求導,求出BD的最大值.
可得到關于BD的函數式,然后通過求導,求出BD的最大值.
試題解析:解:(1)在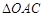 中,
中,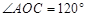 ,
, ,由余弦定理得,
,由余弦定理得,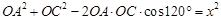 ,
,
又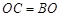 ,所以
,所以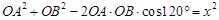 ①,
①,
在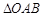 中,
中,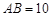 ,
,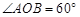
由余弦定理得,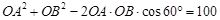 ②, 3分
②, 3分
①+②得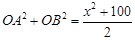 ,①②得
,①②得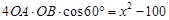 ,即
,即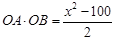 , 4分
, 4分
又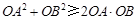 ,所以
,所以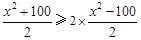 ,即
,即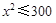 ,
,
又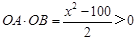 ,即
,即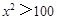 ,所以
,所以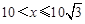 ; 6分
; 6分
(2)易知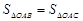 ,故
,故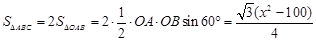 , 8分
, 8分
又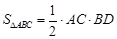 ,設
,設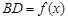 ,所以
,所以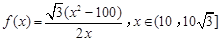 , 9分
, 9分
又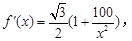 則
則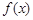 在
在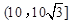 上是增函數,
上是增函數,
所以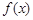 的最大值為
的最大值為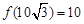 ,即BD的最大值為10. 12分
,即BD的最大值為10. 12分
(利用調性定義證明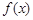 在
在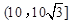 上是增函數,同樣給滿分;如果直接說出
上是增函數,同樣給滿分;如果直接說出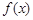
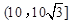 上是增函數,但未給出證明,扣2分.)
上是增函數,但未給出證明,扣2分.)
考點:1.余弦定理;2.函數的導數及其導數性質的應用.


科目:高中數學 來源: 題型:解答題
已知函數f(x)= sin
sin cos
cos +sin2
+sin2 (其中ω>0,0<φ<
(其中ω>0,0<φ< ).其圖象的兩個相鄰對稱中心的距離為
).其圖象的兩個相鄰對稱中心的距離為 ,且過點
,且過點 .
.
(1)函數f(x)的解析式;
(2)在△ABC中,a,b,c分別是角A,B,C的對邊,a= ,S△ABC=2
,S△ABC=2 ,角C為銳角.且滿足f
,角C為銳角.且滿足f =
= ,求c的值.
,求c的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,甲船以每小時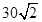 海里的速度向正北方航行,乙船按固定方向勻速直線航行,當甲船位于
海里的速度向正北方航行,乙船按固定方向勻速直線航行,當甲船位于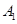 處時,乙船位于甲船的北偏西
處時,乙船位于甲船的北偏西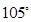 方向的
方向的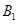 處,此時兩船相距
處,此時兩船相距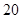 海里,當甲船航行
海里,當甲船航行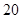 分鐘到達
分鐘到達 處時,乙船航行到甲船的北偏西
處時,乙船航行到甲船的北偏西 方向的
方向的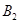 處,此時兩船相距
處,此時兩船相距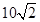 海里,問乙船每小時航行多少海里?
海里,問乙船每小時航行多少海里?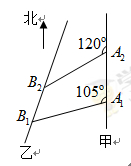
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,山頂有一座石塔 ,已知石塔的高度為
,已知石塔的高度為 .
.
(Ⅰ)若以 為觀測點,在塔頂
為觀測點,在塔頂 處測得地面上一點
處測得地面上一點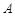 的俯角為
的俯角為 ,在塔底
,在塔底 處測得
處測得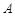 處的俯角為
處的俯角為 ,用
,用 表示山的高度
表示山的高度 ;
;
(Ⅱ)若將觀測點選在地面的直線 上,其中
上,其中 是塔頂
是塔頂 在地面上的射影.已知石塔高度
在地面上的射影.已知石塔高度 ,當觀測點
,當觀測點 在
在 上滿足
上滿足 時看
時看 的視角(即
的視角(即 )最大,求山的高度
)最大,求山的高度 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=cos 2x+2sin x·sin.
(1)求f(x)的最小正周期,最大值以及取得最大值時x的集合;
(2)若A是銳角三角形△ABC的內角,f(A)=0,b=5,a=7,求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com