
某工廠為了對新研發的一種產品進行合理定價,將該產品按事先擬定的價格進行試銷,得到如下數據:
單價 (元) (元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量 (件) (件) | 90 | 84 | 83 | 80 | 75 | 68 |
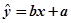 中的
中的 ,據此模型預報單價為10元時的銷量為多少件?
,據此模型預報單價為10元時的銷量為多少件? 成本)
成本) (1)50件;(2)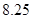 元
元
解析試題分析:(1)由于線性回歸直線方程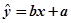 恒過樣本中心點
恒過樣本中心點 ,故選由題中數據求出
,故選由題中數據求出 和
和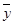 的值,再由已知b=20,代入回歸直線方程
的值,再由已知b=20,代入回歸直線方程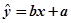 中就可求出a的值,然后令x=10,求得的y的值,即是為預報單價為10元時的銷量;(2)由已知可將工廠的利潤表達成為該產品的單價x的函數,由于該函數是一個二次函數,利用配方法可求出使工廠利潤最大時對應的單價x的值;注意實際應用問題最后一定要回答.
中就可求出a的值,然后令x=10,求得的y的值,即是為預報單價為10元時的銷量;(2)由已知可將工廠的利潤表達成為該產品的單價x的函數,由于該函數是一個二次函數,利用配方法可求出使工廠利潤最大時對應的單價x的值;注意實際應用問題最后一定要回答.
試題解析:(1)由于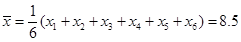 ,
,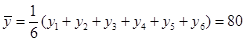 , 4分
, 4分
所以 . 6分
. 6分
從而回歸直線方程為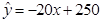 .
.
據此模型,單價為10元時的銷量為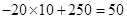 件 8分
件 8分
(2)設工廠獲得的利潤為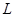 元,依題意得
元,依題意得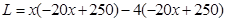
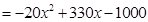
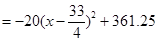 12分
12分
當且僅當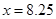 時,
時, 取得最大值.
取得最大值.
故當單價定為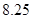 元時,工廠可獲得最大利潤. 14分
元時,工廠可獲得最大利潤. 14分
考點:1.線性回歸;2.二次函數的應用.


科目:高中數學 來源: 題型:解答題
高二某班50名學生在一次百米測試中,成績全部都介于13秒到18秒之間,將測試結果按如下方式分成五組,第一組[13,14),第二組[14,15)…第五組[17,18],如圖是按上述分組方法得到的頻率分布直方圖.
(1)若成績大于等于14秒且小于16秒規定為良好,求該班在這次百米測試中成績為良好的人數.
(2)請根據頻率分布直方圖,估計樣本數據的眾數和中位數(精確到0.01).
(3)設 表示該班兩個學生的百米測試成績,已知
表示該班兩個學生的百米測試成績,已知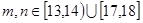 ,求事件
,求事件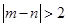 的概率.
的概率.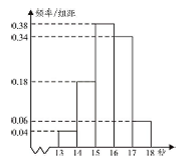
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
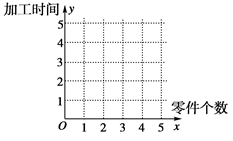
某車間為了規定工時定額,需要確定加工零件所花費的時間,為此作了四次試驗,得到的數據如下:
零件的個數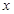 (個) (個) | 2 | 3 | 4 | 5 |
加工的時間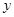 (小時) (小時) | 2.5 | 3 | 4 | 4.5 |
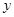 關于
關于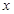 的線性回歸方程
的線性回歸方程 ,并在坐標系中畫出回歸直線;
,并在坐標系中畫出回歸直線;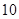 個零件需要多少時間?
個零件需要多少時間? ,其中
,其中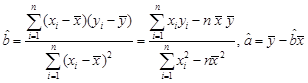 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
“世界睡眠日”定在每年的3月21日,2009年的世界睡眠日主題是“科學管理睡眠”,以提高公眾對健康睡眠的自我管理能力和科學認識.為此某網站于2009年3月13日到3月20日持續一周網上調查公眾日平均睡眠的時間(單位:小時),共有2000人參加調查,現將數據整理分組后如題中表格所示.
序號 | 分組睡眠時間 | 組中值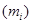 | 頻數 (人數) | 頻率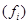 |
| 1 | 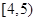 | 4.5 | 80 | ( ) |
| 2 | 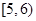 | 5.5 | 520 | 0.26 |
| 3 | 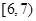 | 6.5 | 600 | 0.30 |
| 4 | 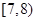 | 7.5 | ( ) | ( ) |
| 5 | 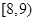 | 8.5 | 200 | 0.10 |
| 6 | 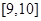 | 9.5 | 40 | 0.02 |
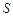 值。
值。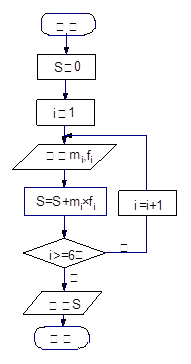
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為調查某市老年人是否需要志愿者提供幫助,用簡單隨機抽樣方法從該市調查了500位老年人,結果如右表.
| 性別 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
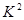
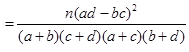 (
(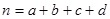 )
)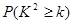 | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某班主任對全班50名學生的積極性和對待班級工作的態度進行了調查,
統計數據如下表所示:
| | 積極參加班級工作 | 不太積極參加班級工作 | 合計 |
| 學習積極性高 | 18 | 7 | 25 |
| 學習積極性一般 | 6 | 19 | 25 |
| 合計 | 24 | 26 | 50 |
|
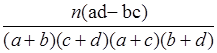
| P(K2≥k0 ) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某電視臺在一次對文藝節目和新聞節目觀眾的抽樣調查中,隨機抽取了100名電視觀眾,相關數據如下表所示:
| | 文藝節目 | 新聞節目 | 總計 |
| 20歲到40歲 | 40 | 20 | 60 |
| 40歲以上 | 15 | 25 | 40 |
| 總計 | 55 | 45 | 100 |
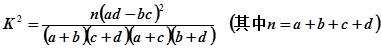
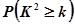 | 0.05 | 0.01 | 0.005 | 0.001 |
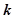 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某種產品的廣告費支出z與銷售額y(單位:萬元)之間有如下對應數據:
若廣告費支出z與銷售額y回歸直線方程為多一6.5z+n(n∈R).
(1)試預測當廣告費支出為12萬元時,銷售額是多少?
(2)在已有的五組數據中任意抽取兩組,求至少有一組數據其預測值與實際值之差的絕對值不超過5的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
已知 某天一工廠甲、乙、丙三個車間生產的產品件數分別是1500、1300、1200,現用分層抽樣方法抽取了一個樣本容量為n的樣本,進行質量檢查,已知丙車間抽取了24件產品,則n=____________.
某天一工廠甲、乙、丙三個車間生產的產品件數分別是1500、1300、1200,現用分層抽樣方法抽取了一個樣本容量為n的樣本,進行質量檢查,已知丙車間抽取了24件產品,則n=____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com