Question

若f(1)=0，f(0)=f(1×0)=f(1)f(0)=0，所以f(1)=f(0)與已知條件“”矛盾所以f(1)≠0，因此f(1)=1,所以f(1)-1=0，1是函數y=f(x)-1的零點

（2）因為f(1)=f[(-1)×（-1）]=f2(-1)=,所以f(-1)=±1，但若f(-1)=1,則f(-1)=f(1)與已知矛盾所以f(-1)不能等于1，只能等于-1。所以任x∈R，f(-x)=f(-1)f(x)=-f(x)，因此函數是奇函數

已知某地每單位面積的菜地年平均使用氮肥量與每單位面積蔬菜年平均產量之間有的關系如下數據：

年份	x(kg)	y(t)
1985	70	5.1
1986	74	6.0
1987	80	6.8
1988	78	7.8
1989	85	9.0
1990	92	10.2
1991	90	10.0
1992	95	12.0
1993	92	11.5
1994	108	11.0
1995	115	11.8
1996	123	12.2
1997	130	12.5
1998	138	12.8
1999	145	13.0

(1)求x與y之間的相關系數，并檢驗是否線性相關；

（2）若線性相關，則求蔬菜產量y與使用氮肥x之間的回歸直線方程，并估計每單位面積施150kg時，每單位面積蔬菜的平均產量.

Answer 1

見解析

解析:

若設，則

所以變量對變量的回歸方程是

若f(1)=0，f(0)=f(1×0)=f(1)f(0)=0，所以f(1)=f(0)與已知條件“”矛盾所以f(1)≠0，因此f(1)=1,所以f(1)-1=0，1是函數y=f(x)-1的零點

（2）因為f(1)=f[(-1)×（-1）]=f2(-1)=,所以f(-1)=±1，但若f(-1)=1,則f(-1)=f(1)與已知矛盾所以f(-1)不能等于1，只能等于-1。所以任x∈R，f(-x)=f(-1)f(x)=-f(x)，因此函數是奇函數

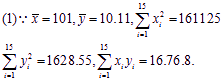 故蔬菜產量與使用氮肥量的相關系數為：

由于，故自由度為15－2＝13，由相關系數檢驗的臨界值表查出與顯著水平0.05及自由度13相關系數臨界值從而可以看出，從而說明蔬菜產量與氮肥使用量之間存在相關關系.

（2）設所求的回歸直線方程為：，則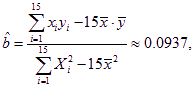

從而所求的回歸直線方程為：

所以當時，

即估計每單位面積施肥150（t）時，每單位面積蔬菜的年平均產量為