
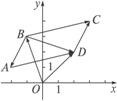
圖3
活動:本例的目的仍然是讓學生熟悉平面向量的坐標運算.這里給出了兩種解法:解法一利用“兩個向量相等,則它們的坐標相等”,解題過程中應用了方程思想;解法二利用向量加法的平行四邊形法則求得向量![]() 的坐標,進而得到點D的坐標.解題過程中,關鍵是充分利用圖形中各線段的位置關系(主要是平行關系),數形結合地思考,將頂點D的坐標表示為已知點的坐標.
的坐標,進而得到點D的坐標.解題過程中,關鍵是充分利用圖形中各線段的位置關系(主要是平行關系),數形結合地思考,將頂點D的坐標表示為已知點的坐標.
解:方法一:如圖3,設頂點D的坐標為(x,y).
∵![]() =(-1-(-2),3-1)=(1,2),
=(-1-(-2),3-1)=(1,2),![]() =(3-x,4-y).
=(3-x,4-y).
由![]() =
=![]() ,得(1,2)=(3-x,4-y).
,得(1,2)=(3-x,4-y).
∴![]()
∴![]()
∴頂點D的坐標為(2,2).
方法二:如圖3,由向量加法的平行四邊形法則,可知
![]() =
=![]() +
+![]() =
=![]() +
+![]() =(-2-(-1),1-3)+(3-(-1),4-3)=(3,-1),
=(-2-(-1),1-3)+(3-(-1),4-3)=(3,-1),
而![]() =
=![]() +
+![]() =(-1,3)+(3,-1)=(2,2),
=(-1,3)+(3,-1)=(2,2),
∴頂點D的坐標為(2,2).
點評:本例的目的仍然是讓學生熟悉平面向量的坐標運算.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
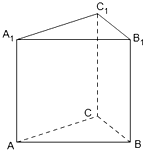 如圖,已知A,B,C為不在同一直線上的三點,且AA1∥BB1∥CC1,AA1=BB1=CC1.
如圖,已知A,B,C為不在同一直線上的三點,且AA1∥BB1∥CC1,AA1=BB1=CC1.查看答案和解析>>
科目:高中數學 來源: 題型:
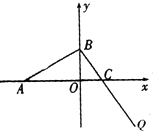 如圖,已知A(-3,0),B、C兩點分別在y軸和x軸上運動,并且滿足
如圖,已知A(-3,0),B、C兩點分別在y軸和x軸上運動,并且滿足| AB |
| BQ |
| BC |
| 1 |
| 2 |
| CQ |
查看答案和解析>>
科目:高中數學 來源: 題型:

(1)求點P的軌跡方程;
(2)經過點C的直線l與點P的軌跡交于M、N兩點,且點C分![]() 所成比等于2∶3,求直線l的方程.
所成比等于2∶3,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源:高考數學階段評估5(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com