
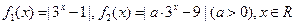 ,
, 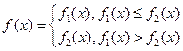 .
.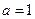 時,求
時,求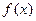 在
在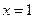 處的切線方程;
處的切線方程;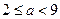 時,設
時,設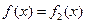 所對應的自變量取值區間的長度為
所對應的自變量取值區間的長度為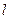 (閉區間
(閉區間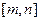 的長度定義為
的長度定義為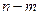 ),試求
),試求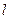 的最大值;
的最大值;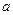 ,使得當
,使得當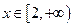 時,
時,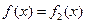 ?若存在,求出
?若存在,求出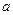 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.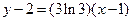 ,
,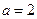 時,
時,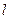 取得最大值為
取得最大值為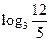
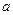 存在,且
存在,且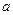 的取值范圍是
的取值范圍是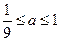
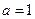 時,
時,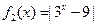 .
.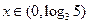 時,
時,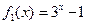 ,
,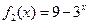 ,
,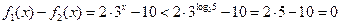 ,
,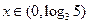 時,
時,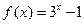 ,且
,且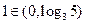 …………………………(3分)
…………………………(3分)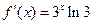 ,所以
,所以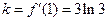 ,又
,又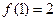 ,
,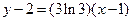 ,
,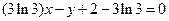 ………………………………………………………(5分)
………………………………………………………(5分)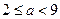 ,所以
,所以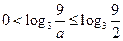 ,則
,則 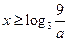 時,因為
時,因為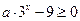 ,
,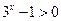 ,
,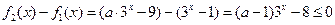 ,解得
,解得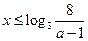 ,
,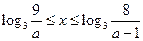 時,
時,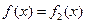 …………………………………(6分)
…………………………………(6分)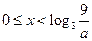 時,因為
時,因為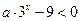 ,
,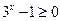 ,
,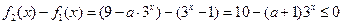 ,解得
,解得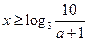 ,
,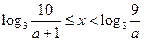 時,
時,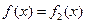 ……………………………(7分)
……………………………(7分)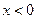 時,因為
時,因為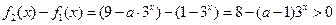 ,
,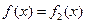 一定不成立………………………………………………………(8分)
一定不成立………………………………………………………(8分)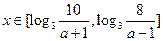 時,
時,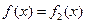 ,
,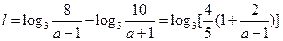 …………………………………(9分)
…………………………………(9分)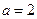 時,
時,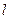 取得最大值為
取得最大值為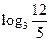 ………………………………………(10分)
………………………………………(10分)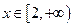 時,
時,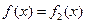 ”等價于“
”等價于“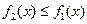 對
對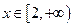 恒成立”,
恒成立”,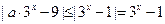 (*)對
(*)對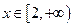 恒成立” ……………………(11分)
恒成立” ……………………(11分)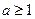 時,
時,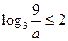 ,則當
,則當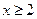 時,
時,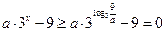 ,則(*)可化為
,則(*)可化為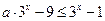 ,即
,即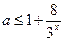 ,而當
,而當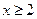 時,
時,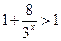 ,
,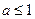 ,從而
,從而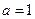 適合題意……………………………………………………(12分)
適合題意……………………………………………………(12分)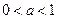 時,
時,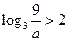 .
.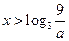 時,(*)可化為
時,(*)可化為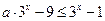 ,即
,即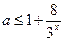 ,而
,而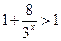 ,
,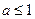 ,此時要求
,此時要求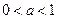 ……………………………………………(13分)
……………………………………………(13分)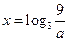 時,(*)可化為
時,(*)可化為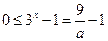 ,
,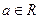 ,此時只要求
,此時只要求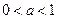 ……………………………………………(14分)
……………………………………………(14分)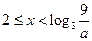 時,(*)可化為
時,(*)可化為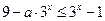 ,即
,即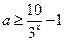 ,而
,而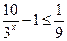 ,
,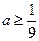 ,此時要求
,此時要求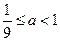 ……………………………………………(15分)
……………………………………………(15分)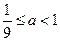 符合題意要求.
符合題意要求.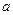 存在,且
存在,且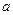 的取值范圍是
的取值范圍是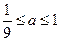 ……………………(16分)
……………………(16分)

科目:高中數學 來源:不詳 題型:解答題
 的廠房(不管墻高),工程的造價是:
的廠房(不管墻高),工程的造價是:查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 的正方形
的正方形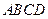
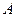 為圓心作半徑為
為圓心作半徑為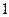 的圓弧與正方形交于
的圓弧與正方形交于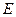 、
、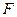 兩點,在
兩點,在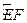 上有一動點
上有一動點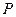 ,過
,過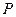 作
作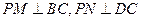 ,求矩形
,求矩形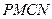 面積的最小值;
面積的最小值;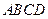 的基礎上再拼接兩個完全相同的正方形,求
的基礎上再拼接兩個完全相同的正方形,求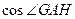 。
。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com