
(1)求點P(x,y)的軌跡方程;
(2)若直線l:y=kx+m(m≠0)與曲線C交于A、B兩點,D(0,-1)且有|![]() |=|
|=|![]() |,試求實數m的取值范圍.
|,試求實數m的取值范圍.
思路分析:本題是解析幾何與平面向量的一道綜合題,仔細分析題意并聯想到a=(x1,y1),b=(x2,y2).若a·b=0,則a⊥b即可得.
解:(1)由(a+![]() b)⊥(a-
b)⊥(a-![]() b)得a2-3b2=0.
b)得a2-3b2=0.
∴x2-3(1+y2)=0,即![]() -y2=1.
-y2=1.
∴點P(x,y)的軌跡方程為![]() -y2=1.
-y2=1.
(2)由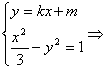 (1-3k2)x2-6kmx-3m2-3=0. ①
(1-3k2)x2-6kmx-3m2-3=0. ①
顯然(1-3k2)≠0且Δ=(6km)2-4(1-3k2)(-3m2-3)=12(m2+1-3k2)>0. ②
設x1、x2為方程①的兩根,則x1+x2=![]() .
.
∴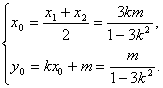
∴AB中點M的坐標為(![]() ).
).
∴線段AB的中垂線的方程為
y-![]() =(-
=(-![]() )(x-
)(x-![]() ).
).
又∵|![]() |=|
|=|![]() |,
|,
∴D(0,-1)是方程的解,代入即得4m=3k2-1,
代入②得12(m2-4m)>0,
即得m<0或m>4.
又∵4m=3k2-1>-1,
∴m>-![]() .
.
故-![]() <m<0或m>4.
<m<0或m>4.


 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| x |
| 3 |
| x |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| x |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com