
已知某個幾何體的三視圖如下,根據(jù)圖中標(biāo)出的尺寸(單位:cm),可得這個幾何體的體積是( )
A.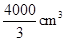 | B.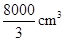 | C.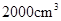 | D. |
B
解析試題分析:先由三視圖得到幾何體的形狀及度量關(guān)系,利用棱錐的體積公式求出體積.
由三視圖可得幾何體是四棱錐V-ABCD,
其中面VCD⊥面ABCD;底面ABCD是邊長為20cm的正方形;棱錐的高是20cm,由棱錐的體積公式得V= Sh=
Sh= ×20×20×20=
×20×20×20=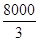 cm3
cm3
故答案為: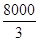 cm3,選B。
cm3,選B。
考點(diǎn):本題主要考查了三視圖的知識,三視圖是新增考點(diǎn), 主要運(yùn)用三視圖還原幾何體的運(yùn)用。
點(diǎn)評:解決該試題的關(guān)鍵是根據(jù)三張圖的關(guān)系,可知幾何體是正方體的一部分,是一個四棱錐.本題也可改編為求該幾何體的外接球的表面積,則必須補(bǔ)全為正方體,增加了難度


 出彩同步大試卷系列答案
出彩同步大試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:單選題
如圖,四棱錐S—ABCD的底面為正方形,SD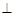 底面ABCD,則下列結(jié)論中不正確的是
底面ABCD,則下列結(jié)論中不正確的是
| A.AC⊥SB |
| B.AB∥平面SCD |
| C.SA與平面SBD所成的角等于SC與平面SBD所成的角 |
| D.AB與SC所成的角等于DC與SA所成的角 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
下列幾何體中是旋轉(zhuǎn)體的是
①圓柱;②六棱錐;③正方體;④球體;⑤四面體.
| A.①和⑤ | B.① | C.③和④ | D.①和④ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
把正方形 沿對角線
沿對角線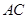 折起,當(dāng)以
折起,當(dāng)以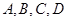 四點(diǎn)為頂點(diǎn)的三棱錐體積最大時,直線
四點(diǎn)為頂點(diǎn)的三棱錐體積最大時,直線 和平面
和平面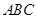 所成的角的大小為( )
所成的角的大小為( )
A.90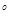 | B.30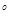 | C.60 | D.45 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com