
(本小題滿(mǎn)分13分)設(shè)橢圓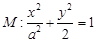
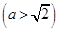 的右焦點(diǎn)為
的右焦點(diǎn)為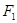 ,直線(xiàn)
,直線(xiàn)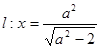 與
與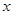 軸交于點(diǎn)
軸交于點(diǎn)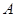 ,若
,若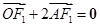 (其中
(其中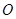 為坐標(biāo)原點(diǎn)).
為坐標(biāo)原點(diǎn)).
(1)求橢圓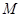 的方程;
的方程;
(2)設(shè)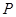 是橢圓
是橢圓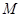 上的任意一點(diǎn),
上的任意一點(diǎn),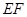 為圓
為圓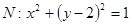 的任意一條直徑(
的任意一條直徑( 、
、 為直徑的兩個(gè)端點(diǎn)),求
為直徑的兩個(gè)端點(diǎn)),求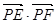 的最大值.
的最大值.
(1)橢圓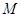 的方程為
的方程為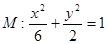 .
(2)
.
(2)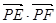 的最大值為11.
的最大值為11.
【解析】(1) 由題設(shè)知,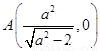 ,
, ,由
,由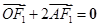 ,得
,得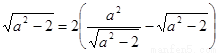 ,從而得到關(guān)于a的方程,求出a值.
,從而得到關(guān)于a的方程,求出a值.
(2)設(shè)圓 的圓心為
的圓心為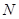 ,則
,則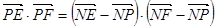

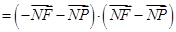
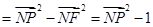 ,
,
從而把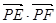 的最大值轉(zhuǎn)化為求
的最大值轉(zhuǎn)化為求 的最大值,再利用兩點(diǎn)間的距離公式再借助P在橢圓上,可以把
的最大值,再利用兩點(diǎn)間的距離公式再借助P在橢圓上,可以把 轉(zhuǎn)化為關(guān)于P的橫坐標(biāo)x的函數(shù)問(wèn)題來(lái)解決.
轉(zhuǎn)化為關(guān)于P的橫坐標(biāo)x的函數(shù)問(wèn)題來(lái)解決.
(1)由題設(shè)知,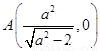 ,
, ,………………………1分
,………………………1分
由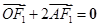 ,得
,得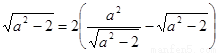 .………………3分
.………………3分
解得 .所以橢圓
.所以橢圓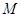 的方程為
的方程為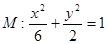 .…………………4分
.…………………4分
(2)方法1:設(shè)圓 的圓心為
的圓心為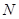 ,
,
則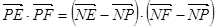 ……………………6分
……………………6分

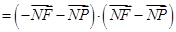 ……K…………………………7分
……K…………………………7分
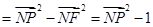 .………………………………………8分
.………………………………………8分
從而求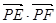 的最大值轉(zhuǎn)化為求
的最大值轉(zhuǎn)化為求 的最大值.………………………9分
的最大值.………………………9分
因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012111916322208205071/SYS201211191633388163231372_DA.files/image017.png">是橢圓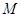 上的任意一點(diǎn),設(shè)
上的任意一點(diǎn),設(shè)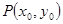 ,……………………………10分
,……………………………10分
所以 ,即
,即 .…………………………11分
.…………………………11分
因?yàn)辄c(diǎn)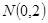 ,所以
,所以 .……………12分
.……………12分
因?yàn)?img
src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012111916322208205071/SYS201211191633388163231372_DA.files/image023.png">,所以當(dāng)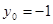 時(shí),
時(shí), 取得最大值12.……………13分
取得最大值12.……………13分
所以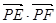 的最大值為11.……………………………14分
的最大值為11.……………………………14分
方法2:設(shè)點(diǎn)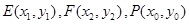 ,
,
因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012111916322208205071/SYS201211191633388163231372_DA.files/image026.png">的中點(diǎn)坐標(biāo)為 ,所以
,所以 …………………………6分
…………………………6分
所以 ……………………7分
……………………7分
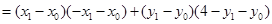

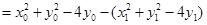 .……………………………9分
.……………………………9分
因?yàn)辄c(diǎn) 在圓
在圓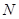 上,所以
上,所以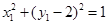 ,即
,即 .…………10分
.…………10分
因?yàn)辄c(diǎn)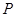 在橢圓
在橢圓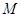 上,所以
上,所以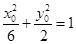 ,即
,即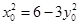 .………………11分
.………………11分
所以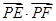
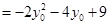
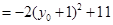 .……………………………12分
.……………………………12分
因?yàn)?img
src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012111916322208205071/SYS201211191633388163231372_DA.files/image041.png">,所以當(dāng)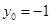 時(shí),
時(shí),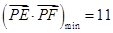 .…………………14分
.…………………14分
方法3:①若直線(xiàn)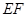 的斜率存在,設(shè)
的斜率存在,設(shè)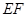 的方程為
的方程為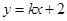 ,……………6分
,……………6分
由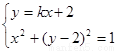 ,解得
,解得 .………………………7分
.………………………7分
因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012111916322208205071/SYS201211191633388163231372_DA.files/image017.png">是橢圓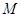 上的任一點(diǎn),設(shè)點(diǎn)
上的任一點(diǎn),設(shè)點(diǎn)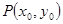 ,
,
所以 ,即
,即 .…………………8分
.…………………8分
所以 ………9分
………9分
所以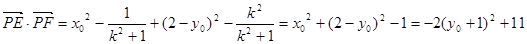 .
.
………10分
因?yàn)?img
src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012111916322208205071/SYS201211191633388163231372_DA.files/image023.png">,所以當(dāng)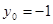 時(shí),
時(shí),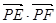 取得最大值11.……………11分
取得最大值11.……………11分
②若直線(xiàn)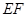 的斜率不存在,此時(shí)
的斜率不存在,此時(shí)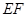 的方程為
的方程為 ,
,
由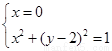 ,解得
,解得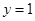 或
或 .
.
不妨設(shè),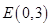 ,
,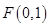 .……………………5u…………………12分
.……………………5u…………………12分
因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012111916322208205071/SYS201211191633388163231372_DA.files/image017.png">是橢圓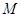 上的任一點(diǎn),設(shè)點(diǎn)
上的任一點(diǎn),設(shè)點(diǎn)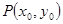 ,
,
所以 ,即
,即 .
.
所以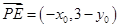 ,
,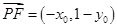 .
.
所以 .
.
因?yàn)?img
src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012111916322208205071/SYS201211191633388163231372_DA.files/image023.png">,所以當(dāng)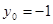 時(shí),
時(shí),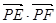 取得最大值11.………13分
取得最大值11.………13分
綜上可知,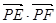 的最大值為11.…………………………………14分
的最大值為11.…………………………………14分


 備戰(zhàn)中考寒假系列答案
備戰(zhàn)中考寒假系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:2015屆江西省高一第二次月考數(shù)學(xué)試卷(解析版) 題型:解答題
(本小題滿(mǎn)分13分)已知函數(shù)
 .
.
(1)求函數(shù) 的最小正周期和最大值;
的最小正周期和最大值;
(2)在給出的直角坐標(biāo)系中,畫(huà)出函數(shù) 在區(qū)間
在區(qū)間 上的圖象.
上的圖象.
(3)設(shè)0<x< ,且方程
,且方程 有兩個(gè)不同的實(shí)數(shù)根,求實(shí)數(shù)m的取值范圍.
有兩個(gè)不同的實(shí)數(shù)根,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年福建省高三年級(jí)八月份月考試卷理科數(shù)學(xué) 題型:解答題
(本小題滿(mǎn)分13分)已知定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052519321600001521/SYS201205251933396875338731_ST.files/image001.png">的函數(shù) 是奇函數(shù).
是奇函數(shù).
(1)求 的值;(2)判斷函數(shù)
的值;(2)判斷函數(shù) 的單調(diào)性;
的單調(diào)性;
(3)若對(duì)任意的 ,不等式恒成立
,不等式恒成立 ,求k的取值范圍.
,求k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年福建省高三年級(jí)八月份月考試卷理科數(shù)學(xué) 題型:解答題
(本小題滿(mǎn)分13分)已知集合 ,
,  ,
, .
.
(1)求 (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:河南省09-10學(xué)年高二下學(xué)期期末數(shù)學(xué)試題(理科) 題型:解答題
(本小題滿(mǎn)分13分)如圖,正三棱柱 的所有棱長(zhǎng)都為2,
的所有棱長(zhǎng)都為2, 為
為 的中點(diǎn)。
的中點(diǎn)。
(Ⅰ)求證: ∥平面
∥平面 ;
;
(Ⅱ)求異面直線(xiàn) 與
與 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

[來(lái)源:KS5
U.COM
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2010-2011學(xué)年福建省高三5月月考調(diào)理科數(shù)學(xué) 題型:解答題
(本小題滿(mǎn)分13分)
已知 為銳角,且
為銳角,且 ,函數(shù)
,函數(shù) ,數(shù)列{
,數(shù)列{ }的首項(xiàng)
}的首項(xiàng) .
.
(1) 求函數(shù) 的表達(dá)式;
的表達(dá)式;
(2)在 中,若
中,若 A=2
A=2 ,
, ,BC=2,求
,BC=2,求 的面積
的面積
(3) 求數(shù)列 的前
的前 項(xiàng)和
項(xiàng)和
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com