
在△ABC中,角A、B、C的對邊分別是 .已知
.已知
(1)求角C的大小;
(2)若 ,求△ABC外接圓半徑.
,求△ABC外接圓半徑.
(1) (2)
(2)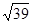 .
.
解析試題分析:(1)由三角函數(shù)給值求角知識可知:要求角的大小,首先必須明確角的范圍,再就是求出角的某一三角函數(shù)值;因此既然是求角C,而已知等式 中只含有角C,所以只須將cosC移到等式的右側(cè),逆用余弦倍角公式,左邊用正弦的倍角公式化成
中只含有角C,所以只須將cosC移到等式的右側(cè),逆用余弦倍角公式,左邊用正弦的倍角公式化成 再注意到
再注意到 ,從而可得
,從而可得 ,然后兩邊一平方就可求得sinC=
,然后兩邊一平方就可求得sinC= ,但不能就此得到角C為
,但不能就此得到角C為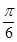 ,還必須注意到
,還必須注意到 ,所以
,所以 (2)由正弦定理可知:△ABC外接圓半徑R滿足
(2)由正弦定理可知:△ABC外接圓半徑R滿足 ,由(1)知角C的大小,所以只需求出邊c即可;注意觀察已知等式
,由(1)知角C的大小,所以只需求出邊c即可;注意觀察已知等式 知可分別按邊a,b配方得到
知可分別按邊a,b配方得到 從而得到
從而得到 再用余弦定理
再用余弦定理 就可求出邊c,進(jìn)而就可求得三角形的外接圓半徑.
就可求出邊c,進(jìn)而就可求得三角形的外接圓半徑.
試題解析:(1)∵ 即
即
由 ,∴
,∴ ,即
,即
∵ ,得
,得 即
即 ,所以
,所以
(2)由 得
得 得
得
∴ ∴
∴ .
.
考點(diǎn):1.三角公式;2.正弦定理和余弦定理.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
地面上有兩座塔AB、CD,相距120米,一人分別在兩塔底部測得一塔頂仰角為另一塔頂仰角的2倍,在兩塔底連線的中點(diǎn)O測得兩塔頂?shù)难鼋腔橛嘟牵髢勺母叨取?br />
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在△ABC中,角A,B,C所對的邊分別為 ,設(shè)S為△ABC的面積,且
,設(shè)S為△ABC的面積,且 。
。
(Ⅰ)求角A的大小;
(Ⅱ)若 ,求△ABC周長的取值范圍.
,求△ABC周長的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在△ABC中,A、B、C所對的邊分別是a、b、c,bcos B是acos C,ccos A的等差中項(xiàng).
(1)求B的大小;
(2)若 ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在△ABC中,內(nèi)角A,B,C所對的邊分別為a,b,c,已知sin B(tan A+tan C)=tan Atan C.
(1)求證:a,b,c成等比數(shù)列;
(2)若a=1,c=2,求△ABC的面積S.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
設(shè) 上的奇函數(shù),且在區(qū)間(0,
上的奇函數(shù),且在區(qū)間(0, )上單調(diào)遞增,若
)上單調(diào)遞增,若 ,三
,三 角形的內(nèi)角A滿足
角形的內(nèi)角A滿足 ,則A的取值范圍是
,則A的取值范圍是
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com