
已知cosα=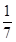 ,cos(α-β)=
,cos(α-β)=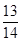 ,且0<β<α<
,且0<β<α<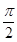 .
.
(1)求tan2α的值;
(2)求β的值.
(1) -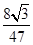 (2)
(2) 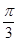
【解析】本試題主要是考查了兩角和差的三角函數變換的運用,以及構造角的思想求解角的 綜合運用。
(1)由cosα=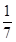 ,0<α<
,0<α<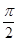 ,
,
得sinα=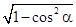 =
=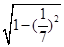 =
=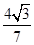 ,
,
∴tanα=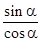 =
=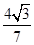 ×
×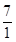 =
=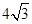 .
.
從而結合二倍角公式得到結論。
(2)由β=α-(α-β)
cosβ=cos[α-(α-β)]
=cosαcos(α-β)+sinαsin(α-β)= 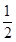
那么利用由0<β<α<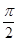 ,得0<α-β<
,得0<α-β<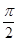 .
.
又∵cos(α-β)=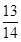 ,得到各個三角函數值,求解得到結論。
,得到各個三角函數值,求解得到結論。
(1)由cosα=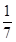 ,0<α<
,0<α<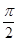 ,
,
得sinα=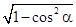 =
=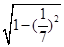 =
=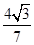 ,
,
∴tanα=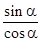 =
=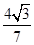 ×
×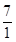 =
=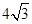 .
.
于是tan2α=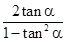 =
=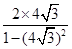
=-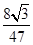 . ………6分
. ………6分
(2)由0<β<α<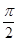 ,得0<α-β<
,得0<α-β<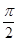 .
.
又∵cos(α-β)=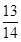 ,
,
∴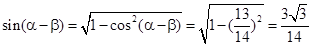
由β=α-(α-β)
cosβ=cos[α-(α-β)]
=cosαcos(α-β)+sinαsin(α-β)= 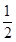
又∵0<β<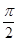
∴β= 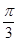 ……13分
……13分


 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數學 來源:2013-2014學年河南省原名校高三上學期期聯考理科數學試卷(解析版) 題型:選擇題
已知向量 =(cosθ,sinθ),向量
=(cosθ,sinθ),向量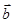 =(
=(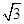 ,-1),則|2
,-1),則|2 -
-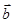 |的最大值與最小值的和是( )
|的最大值與最小值的和是( )
A.4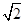 B.6
C.4
D.16
B.6
C.4
D.16
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com