分析:(1)利用條件得PF1⊥PF2以及PF1|2+|PF2|2=(2c)2=16m2.再利用橢圓定義求出關于m的方程,解出m的值就可求橢圓C的左,右焦點F1、F2.
(2)把已知條件轉化為|QF1|2=2(|QF2|2-1),整理即可求出動點Q的軌跡方程.
解答:解:(1)∵c
2=a
2-b
2,∴c
2=4m
2.(2分)
又∵
•=0∴PF
1⊥PF
2,(3分)
∴|PF
1|
2+|PF
2|
2=(2c)
2=16m
2.(5分)
由橢圓定義可知
|PF1|+|PF2|=2a=2m,(|PF
1|+|PF
2|)
2=16m
2+16=24m
2,(6分)
從而得m
2=2,c
2=4m
2=8,c=2
.∴F
1(-2
,0)、F
2(2
,0).(7分)
(2)∵F
1(-2
,0),F
2(2
,0),
由已知:
|QF1|=|QM|,即|QF
1|
2=2|QM|
2,
所以有:|QF
1|
2=2(|QF
2|
2-1),設點Q(x,y),(9分)
則(x+2
)
2+y
2=2[(x-2
)
2+y
2-1],(12分)
即(x-6
)
2+y
2=66)
綜上所述,所求軌跡方程為:(x-6
)
2+y
2=66.(14分)
點評:本題涉及到求動點的軌跡方程問題.在求動點的軌跡方程時,一般是利用條件得到關于動點的等式整理就可求出對應動點的軌跡方程.

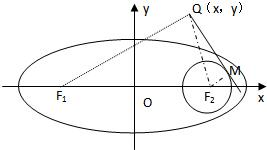 設F1,F2分別是橢圓C:
設F1,F2分別是橢圓C:

 設F1、F2分別是橢圓C:
設F1、F2分別是橢圓C: