
(本小題12分)如圖,甲船以每小時30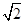 海里的速度向正北方向航行,乙船按固定方向勻速直線航行.當甲船位于A1處時,乙船位于甲船的北偏西105°方向的B1處,此時兩船相距20海里.當甲船航行20分鐘到達A2處時,乙船航行到甲船的北偏西120°方向的B2處,此時兩船相距10
海里的速度向正北方向航行,乙船按固定方向勻速直線航行.當甲船位于A1處時,乙船位于甲船的北偏西105°方向的B1處,此時兩船相距20海里.當甲船航行20分鐘到達A2處時,乙船航行到甲船的北偏西120°方向的B2處,此時兩船相距10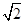 海里,問乙船每小時航行多少海里?
海里,問乙船每小時航行多少海里?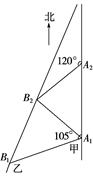
乙船每小時航行30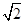 海里
海里
解析試題分析:如圖所示,連結A1B2. 
由已知A2B2=10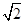 ,A1A2=30
,A1A2=30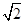 ×
×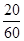 =10
=10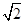 ,
,
∴A1A2=A2B2.又∠A1A2B2=180°-120°=60°,
∴△A1A2B2是等邊三角形,
∴A1B2=A1A2=10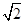 .
.
由已知A1B1=20,∠B1A1B2=105°-60°=45°.
在△A1B2B1中,由余弦定理得
=202+(10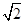 )2-2×20×10
)2-2×20×10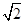 ×
×
=200,
∴B1B2=10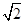 .
.
因此,乙船的速度為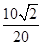 ×60=30
×60=30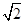 (海里/小時).
(海里/小時).
答:乙船每小時航行30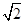 海里
海里
考點:解三角形的運用
點評:解決的關鍵是通過作圖來得到對應的三角形,然后分析邊和角,結合余弦定理來求解得到,屬于基礎題。


科目:高中數學 來源: 題型:解答題
已知函數
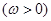 在區間
在區間 上單調遞增,在區間
上單調遞增,在區間 上單調遞減;如圖,四邊形
上單調遞減;如圖,四邊形 中,
中, ,
, ,
, 為
為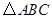 的內角
的內角 的對邊,
的對邊,
且滿足 .
.
(Ⅰ)證明: ;
;
(Ⅱ)若 ,設
,設 ,
, ,
, ,求四邊形
,求四邊形 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某觀測站C在城A的南偏西25°的方向上,由A城出發有一條公路,走向是南偏東50°,在C處測得距C為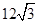 km的公路上B處,有一人正沿公路向A城走去,走了12 km后,到達D處,此時C、D間距離為12 km,問這人還需走多少千米到達A城?
km的公路上B處,有一人正沿公路向A城走去,走了12 km后,到達D處,此時C、D間距離為12 km,問這人還需走多少千米到達A城?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
港口A北偏東30°方向的C處有一檢查站,港口正東方向的B處有一輪船,距離檢查站為31海里,該輪船從B處沿正西方向航行20海里后到達D處觀測站,已知觀測站與檢查站距離21海里,問檢查站C離港口A有多遠?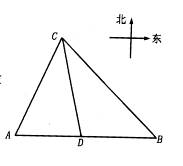
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com