
 ,則下列結(jié)論正確的是 ( )
,則下列結(jié)論正確的是 ( )A.把 的圖象向左平移 的圖象向左平移 個單位,得到一個偶函數(shù)的圖象 個單位,得到一個偶函數(shù)的圖象 |
B. 的圖象關(guān)于點 的圖象關(guān)于點 對稱 對稱 |
C. 的圖象關(guān)于直線 的圖象關(guān)于直線 對稱 對稱 |
D. 的最小正周期為 的最小正周期為 ,且在 ,且在 上為增函數(shù) 上為增函數(shù) |
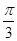 )的對稱軸為2x+
)的對稱軸為2x+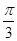 =kπ+
=kπ+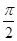 (k∈Z),即x=
(k∈Z),即x=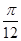 +
+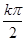 (k∈Z)∴直線x=
(k∈Z)∴直線x=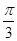 不是函數(shù)f(x)的對稱軸,結(jié)論(3)錯誤
不是函數(shù)f(x)的對稱軸,結(jié)論(3)錯誤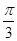 )的對稱中心橫坐標為2x+
)的對稱中心橫坐標為2x+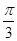 =kπ,即x=
=kπ,即x=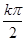 -
-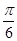 ,∴點(
,∴點(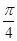 ,0)不是函數(shù)的對稱中心.結(jié)論(2)錯誤.
,0)不是函數(shù)的對稱中心.結(jié)論(2)錯誤.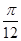 個單位,得f(x)=sin(2x+
個單位,得f(x)=sin(2x+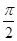 )
)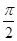 ≤2x+
≤2x+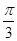 ≤2kπ+
≤2kπ+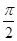 時,即kπ-
時,即kπ-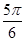 ≤x≤kπ+
≤x≤kπ+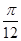


 智趣寒假作業(yè)云南科技出版社系列答案
智趣寒假作業(yè)云南科技出版社系列答案國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com