
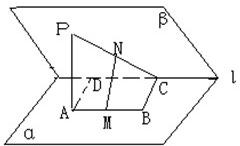
 如圖:在二面角α-l-β中,A、B∈α,C、D∈l,ABCD為矩形,p∈β,PA⊥α,且PA=AD,M、N依次是AB、PC的中點,
如圖:在二面角α-l-β中,A、B∈α,C、D∈l,ABCD為矩形,p∈β,PA⊥α,且PA=AD,M、N依次是AB、PC的中點,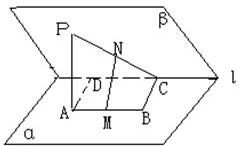 連接NE,
連接NE, DC=AM.FN∥DC∥AM.
DC=AM.FN∥DC∥AM. ∠PAD=45°(等腰直角三角形DAP上直角的一半).
∠PAD=45°(等腰直角三角形DAP上直角的一半).

科目:高中數學 來源: 題型:
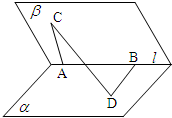 如圖,在二面角α-l-β的棱l上有A,B兩點,直線AC,BD分別在這個二面角的兩個半平面內,且都垂直于AB,若AB=4,AC=6,BD=8,CD=2
如圖,在二面角α-l-β的棱l上有A,B兩點,直線AC,BD分別在這個二面角的兩個半平面內,且都垂直于AB,若AB=4,AC=6,BD=8,CD=2| 17 |
查看答案和解析>>
科目:高中數學 來源: 題型:
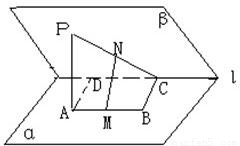
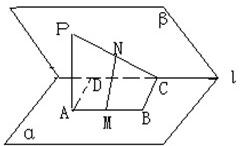 如圖:在二面角α-l-β中,A、B∈α,C、D∈l,ABCD為矩形,p∈β,PA⊥α,且PA=AD,M、N依次是AB、PC的中點,
如圖:在二面角α-l-β中,A、B∈α,C、D∈l,ABCD為矩形,p∈β,PA⊥α,且PA=AD,M、N依次是AB、PC的中點,查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省舟山市岱山縣大衢中學高二(上)10月月考數學試卷(理科)(解析版) 題型:解答題
查看答案和解析>>
科目:高中數學 來源:2009-2010學年湖南省岳陽市華容縣一中高二(上)期末數學試卷(選修2-1及2-2第一節)(解析版) 題型:填空題
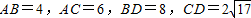 ,則二面角α-l-β的大小為 .
,則二面角α-l-β的大小為 .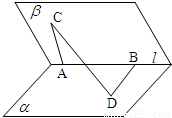
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com