
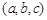 ,如下定義該數組的極差:三個數的最大值與最小值的差.如果
,如下定義該數組的極差:三個數的最大值與最小值的差.如果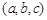 的極差
的極差 ,可實施如下操作
,可實施如下操作 :若
:若 中最大的數唯一,則把最大數減2,其余兩個數各增加1;若
中最大的數唯一,則把最大數減2,其余兩個數各增加1;若 中最大的數有兩個,則把最大數各減1,第三個數加2,此為一次操作,操作結果記為
中最大的數有兩個,則把最大數各減1,第三個數加2,此為一次操作,操作結果記為 ,其級差為
,其級差為 .若
.若 ,則繼續對
,則繼續對 實施操作
實施操作 ,…,實施
,…,實施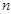 次操作后的結果記為
次操作后的結果記為 ,其極差記為
,其極差記為 .例如:
.例如: ,
,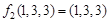 .
. ,求
,求 和
和 的值;
的值; 的極差為
的極差為 且
且 ,若
,若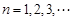 時,恒有
時,恒有 ,求
,求 的所有可能取值;
的所有可能取值; 是以4為公比的正整數等比數列中的任意三項,求證:存在
是以4為公比的正整數等比數列中的任意三項,求證:存在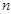 滿足
滿足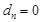 .
.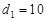 ,
,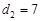 ,
,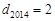 ;(2)
;(2)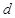 的取值僅能是2;(3)詳見解析.
的取值僅能是2;(3)詳見解析.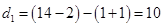 ,這時三數為
,這時三數為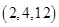 ,第二次操作后,
,第二次操作后,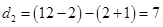 ,這時三數為
,這時三數為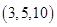 ,第三次操作后,
,第三次操作后,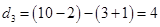 ,,這時三數為
,,這時三數為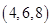 ,第四次操作后,
,第四次操作后,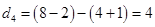 ,這時三數為
,這時三數為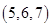 ,第五次操作后,
,第五次操作后,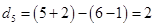 ,這時三數為
,這時三數為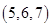 ,第六次操作后,
,第六次操作后,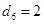 ,這時三數為
,這時三數為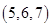 ,
,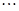 ,第2014次操作后,
,第2014次操作后,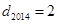 ,這時三數為
,這時三數為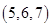 ;(2)已知
;(2)已知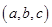 的極差為
的極差為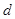 且
且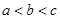 ,這時極差
,這時極差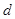 最小值為
最小值為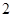 ,當
,當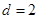 時,這時
時,這時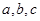 是三個連續的正整數,即為
是三個連續的正整數,即為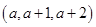 ,由(1)可知,通過變化后,所得數仍然是
,由(1)可知,通過變化后,所得數仍然是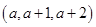 ,所以數組的極差不會改變,即
,所以數組的極差不會改變,即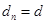 ,符合題意,當
,符合題意,當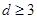 ,這時
,這時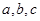 三個數,通過變化成
三個數,通過變化成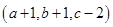 ,這是極差為
,這是極差為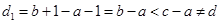 ,或
,或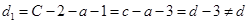 ,這樣就可以確定出
,這樣就可以確定出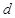 的取值僅能是2;(3)若
的取值僅能是2;(3)若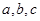 是以4為公比的正整數等比數列中的任意三項,求證:存在
是以4為公比的正整數等比數列中的任意三項,求證:存在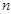 滿足
滿足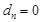 ,這時
,這時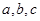 三數形式為
三數形式為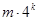 ,由二項式定理可知
,由二項式定理可知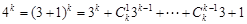 ,故所以
,故所以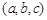 的極差
的極差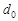 是3的倍數,這樣根據極差的定義,通過操作,得到
是3的倍數,這樣根據極差的定義,通過操作,得到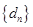 是一個公差為
是一個公差為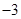 的等差數列,從而可得出結論.
的等差數列,從而可得出結論.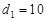 ,
,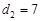 ,
,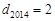 3分
3分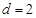 時,則
時,則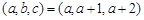
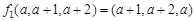 ,
,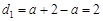 ,
,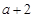 變為最小數
變為最小數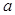 ,最小數
,最小數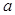 和次
和次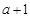 分別變為次小數
分別變為次小數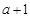 和最大數
和最大數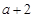 ,所以數組的極差不會改變.
,所以數組的極差不會改變.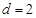 時,
時,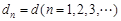 恒成立.
恒成立.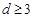 時,則
時,則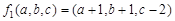
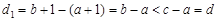 或
或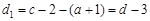
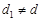 .
.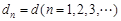 的
的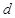 的取值僅能是2. 8分
的取值僅能是2. 8分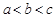 ,所以數組
,所以數組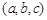 的極差
的極差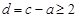
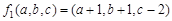 ,
,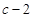 為最大數,則
為最大數,則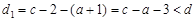
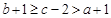 ,則
,則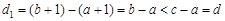
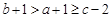 ,則
,則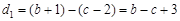 ,
,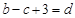 時,可得
時,可得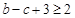 ,即
,即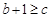
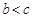 可得
可得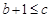
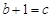
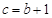 代入
代入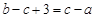 得
得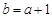
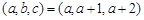 時,
時,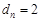 (
(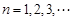 )
)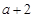 變為最小數
變為最小數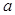 ,最小數
,最小數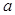 和次小
和次小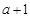 分別變為次小數
分別變為次小數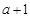 和最大數
和最大數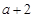 ,所以數組的極差不會改變.
,所以數組的極差不會改變.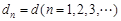 的
的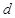 的取值僅能是2. 8分
的取值僅能是2. 8分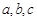 是以4為公比的正整數等比數列的三項,
是以4為公比的正整數等比數列的三項,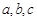 是形如
是形如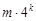 (其中
(其中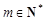 )的數,
)的數,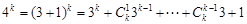
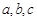 中每兩個數的差都是3的倍數.
中每兩個數的差都是3的倍數.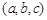 的極差
的極差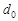 是3的倍數. 9分
是3的倍數. 9分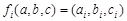 ,不妨設
,不妨設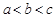 ,
,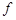 的規則,當在三元數組
的規則,當在三元數組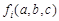 (
(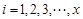 ,
,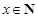 )中,總滿足
)中,總滿足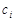 是唯一最大數,
是唯一最大數,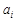 是最小數時,一定有
是最小數時,一定有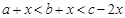 ,解得
,解得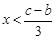 .
.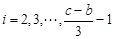 時,
時,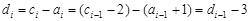 .
.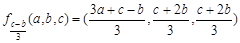 ,
,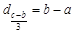
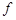 的規則,當在三元數組
的規則,當在三元數組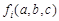 (
(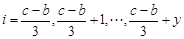 ,
,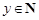 )中,總滿足
)中,總滿足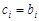 是最大數,
是最大數,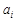 是最小數時,一定有
是最小數時,一定有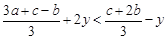 ,解得
,解得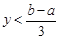 .
.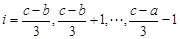 時,
時,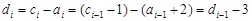 .
.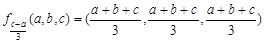 ,
,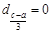
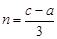 ,滿足
,滿足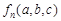 的極差
的極差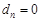 . 13分
. 13分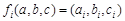 ,則
,則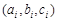 中有唯一最大數時,不妨設
中有唯一最大數時,不妨設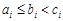 ,則
,則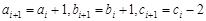 ,
,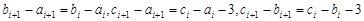
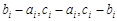 是3的倍數,則
是3的倍數,則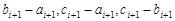 是3的倍數.
是3的倍數.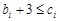 ,則
,則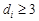 ,
,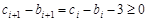 ,
,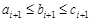
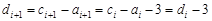 11分
11分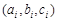 中的最大數有兩個時,不妨設
中的最大數有兩個時,不妨設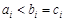 ,則
,則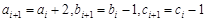 ,
,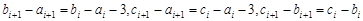 ,
,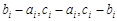 是3的倍數,則
是3的倍數,則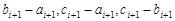 是3的倍數.
是3的倍數.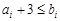 ,則
,則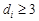 ,
,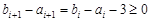
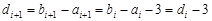 .
.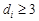 時,數列
時,數列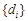 是公差為3的等差數列. 12分
是公差為3的等差數列. 12分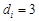 時,由上述分析可得
時,由上述分析可得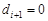 ,此時
,此時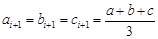
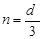 ,滿足
,滿足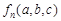 的極差
的極差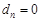 . 13分
. 13分

 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com