
對于定義域為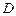 的函數(shù)
的函數(shù)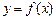 ,若有常數(shù)M,使得對任意的
,若有常數(shù)M,使得對任意的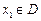 ,存在唯一的
,存在唯一的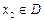 滿足等式
滿足等式 ,則稱M為函數(shù)
,則稱M為函數(shù)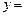 f (x)的“均值”.
f (x)的“均值”.
(1)判斷1是否為函數(shù)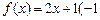 ≤
≤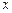 ≤
≤ 的“均值”,請說明理由;
的“均值”,請說明理由;
(2)若函數(shù)
 為常數(shù))存在“均值”,求實數(shù)a的取值范圍;
為常數(shù))存在“均值”,求實數(shù)a的取值范圍;
(3)若函數(shù) 是單調函數(shù),且其值域為區(qū)間I.試探究函數(shù)
是單調函數(shù),且其值域為區(qū)間I.試探究函數(shù) 的“均值”情況(是否存在、個數(shù)、大小等)與區(qū)間I之間的關系,寫出你的結論(不必證明).
的“均值”情況(是否存在、個數(shù)、大小等)與區(qū)間I之間的關系,寫出你的結論(不必證明).
說明:對于(3),將根據(jù)結論的完整性與一般性程度給予不同的評分
解:(1)對任意的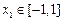 ,有
,有 ,
,
當且僅當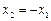 時,有
時,有 ,
,
故存在唯一 ,滿足
,滿足
 , ……………………2分
, ……………………2分
所以1是函數(shù)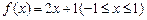 的“均值”. ……………………4分
的“均值”. ……………………4分
(另法:對任意的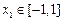 ,有
,有 ,令
,令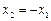 ,
,
則 ,且
,且 ,
,
若 ,且
,且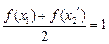 ,則有
,則有 ,可得
,可得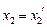 ,
,
故存在唯一 ,滿足
,滿足 , ……………………2分
, ……………………2分
所以1是函數(shù)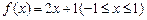 的“
的“ 均值”. ……………………4分)
均值”. ……………………4分)
(2)當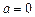 時,
時,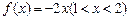 存在“均值”,且“均值”為
存在“均值”,且“均值”為 ;…………5分
;…………5分
當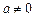 時,由
時,由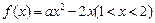 存在均值,可知對任意的
存在均值,可知對任意的 ,
,
都有唯一的 與之對應,從而有
與之對應,從而有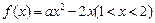 單調,
單調,
故有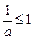 或
或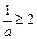 ,解得
,解得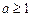 或
或 或
或 , ……………………9分
, ……………………9分
綜上,a的取值范圍是 或
或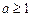 . ……………………10分
. ……………………10分
(另法:分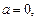
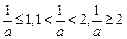 四種情形
四種情形 進行討論)
進行討論)
(3)①當I 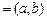 或
或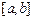 時,函數(shù)
時,函數(shù) 存在唯一的“均值”.
存在唯一的“均值”.
這時函數(shù) 的“均值”為
的“均值”為 ; …………………12分
; …………………12分
②當I為 時,函數(shù)
時,函數(shù) 存在無數(shù)多個“均值”.
存在無數(shù)多個“均值”.
這時任意實數(shù)均為函數(shù) 的“均值”; ……………………14分
的“均值”; ……………………14分
③當I  或
或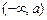 或
或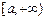 或
或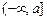 或
或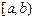 或
或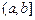 時,
時,
函數(shù) 不存在“均值”. ……………………16分
不存在“均值”. ……………………16分
[評分說明:若三種情況討論完整且正確,但未用等價形式進行敘述,至多得6分;若三種情況討論不完整,且未用等價形式敘述,至多得5分]
①當且僅當I形如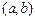 、
、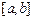 其中之一時,函數(shù)
其中之一時,函數(shù) 存在唯一的“均值”.
存在唯一的“均值”.
這時函數(shù) 的“均值”為
的“均值”為 ; ……………………13分
; ……………………13分
②當且僅當I為 時,函數(shù)
時,函數(shù) 存在無數(shù)多個“均值”.
存在無數(shù)多個“均值”.
這時任意實數(shù)均為函數(shù) 的“均值”;
的“均值”;
解析


 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:高中數(shù)學 來源: 題型:
對于定義域為![]() 的函數(shù)
的函數(shù)![]() ,若同時滿足:①
,若同時滿足:①![]() 在
在![]() 內單調遞增或單調遞減;②存在區(qū)間
內單調遞增或單調遞減;②存在區(qū)間![]()
![]() ,使
,使![]() 在
在![]() 上的值域為
上的值域為![]() ;那么把函數(shù)
;那么把函數(shù)![]() (
(![]() )叫做閉函數(shù).
)叫做閉函數(shù).
(1) 求閉函數(shù)![]() 符合條件②的區(qū)間
符合條件②的區(qū)間![]() ;
;
(2) 若![]() 是閉函數(shù),求實數(shù)
是閉函數(shù),求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(本題滿分14分)定義:對于函數(shù)![]() ,
,![]() .若
.若![]() 對定義域內的
對定義域內的![]() 恒成立,則稱函數(shù)
恒成立,則稱函數(shù)![]() 為
為![]() 函數(shù).(1)請舉出一個定義域為
函數(shù).(1)請舉出一個定義域為![]() 的
的![]() 函數(shù),并說明理由;(2)對于定義域為
函數(shù),并說明理由;(2)對于定義域為![]() 的
的![]() 函數(shù)
函數(shù)![]() ,求證:對于定義域內的任意正數(shù)
,求證:對于定義域內的任意正數(shù)![]() ,均有
,均有![]()
![]() ;
;
(3)對于值域![]() 的
的![]() 函數(shù)
函數(shù)![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆廣東省高一下學期期末考試數(shù)學試卷(解析版) 題型:填空題
對于定義域為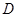 的函數(shù)
的函數(shù)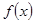 ,若存在區(qū)間
,若存在區(qū)間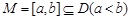 ,使得
,使得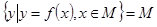 則稱區(qū)間M為函數(shù)
則稱區(qū)間M為函數(shù)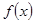 的“等值區(qū)間”.給出下列三個函數(shù):
的“等值區(qū)間”.給出下列三個函數(shù):
① ; ②
; ②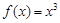 ; ③
; ③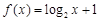
則存在“等值區(qū)間”的函數(shù)的個數(shù)是___________.
查看答案和解析>>
科目:高中數(shù)學 來源:2011-2012學年上海市崇明縣高三第一學期期末考試數(shù)學 題型:填空題
定義:對于定義域為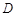 的函數(shù)
的函數(shù)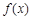 ,如果存在
,如果存在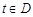 ,使得
,使得 成立,稱函數(shù)
成立,稱函數(shù)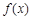 在
在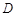 上是“
上是“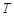 ”函數(shù)。已知下列函數(shù):①
”函數(shù)。已知下列函數(shù):①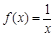 ; ②
; ②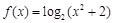 ;③
;③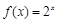 (
(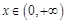 ); ④
); ④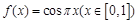 ,其中屬于“
,其中屬于“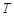 ”函數(shù)的序號是 .(寫出所有滿足要求的函數(shù)的序號)
”函數(shù)的序號是 .(寫出所有滿足要求的函數(shù)的序號)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com