
某公司以每噸10萬元的價格銷售某種產品,每年可售出該產品1000噸,若將該產品每噸的價格上漲x%,則每年的銷售數量將減少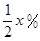 ,該產品每噸的價格上漲百分之幾,可使銷售的總金額最大?
,該產品每噸的價格上漲百分之幾,可使銷售的總金額最大?
 作業輔導系列答案
作業輔導系列答案 同步學典一課多練系列答案
同步學典一課多練系列答案 經典密卷系列答案
經典密卷系列答案科目:高中數學 來源: 題型:解答題
已知函數f(x)的圖象與函數h(x)=x+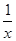 +2的圖象關于點A(0,1)對稱.
+2的圖象關于點A(0,1)對稱.
(1)求f(x)的解析式;
(2)若g(x)=f(x)·x+ax,且g(x)在區間[0,2]上為減函數,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數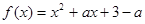 ,
,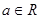 .
.
(1)求 的取值范圍,使
的取值范圍,使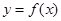 在閉區間
在閉區間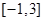 上是單調函數;
上是單調函數;
(2)當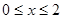 時,函數
時,函數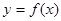 的最大值是關于
的最大值是關于 的函數
的函數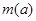 .求
.求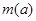 ;
;
(3)求實數 的取值范圍,使得對任意的
的取值范圍,使得對任意的
 ,恒有
,恒有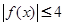 成立.
成立.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某通訊公司需要在三角形地帶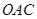 區域內建造甲、乙兩種通信信號加強中轉站,甲中轉站建在區域
區域內建造甲、乙兩種通信信號加強中轉站,甲中轉站建在區域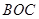 內,乙中轉站建在區域
內,乙中轉站建在區域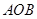 內.分界線
內.分界線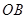 固定,且
固定,且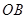 =
=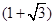 百米,邊界線
百米,邊界線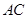 始終過點
始終過點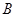 ,邊界線
,邊界線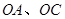 滿足
滿足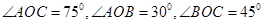 .
.
設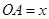 (
(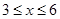 )百米,
)百米,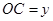 百米.
百米.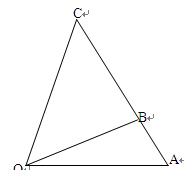
(1)試將 表示成
表示成 的函數,并求出函數
的函數,并求出函數 的解析式;
的解析式;
(2)當 取何值時?整個中轉站的占地面積
取何值時?整個中轉站的占地面積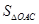 最小,并求出其面積的最小值.
最小,并求出其面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對于函數 ,若在定義域存在實數
,若在定義域存在實數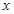 ,滿足
,滿足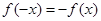 ,則稱
,則稱 為“局部奇函數”.
為“局部奇函數”.
(1)已知二次函數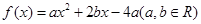 ,試判斷
,試判斷 是否為“局部奇函數”?并說明理由;
是否為“局部奇函數”?并說明理由;
(2)設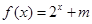 是定義在
是定義在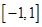 上的“局部奇函數”,求實數
上的“局部奇函數”,求實數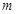 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知兩條直線l1:y=m和l2:y=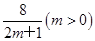 ,l1與函數y=|log2x|的圖象從左至右相交于點A、B,l2與函數y=|log2x|的圖象從左至右相交于點C、D.記線段AC和BD在x軸上的投影長度分別為a、b.當m變化時,求
,l1與函數y=|log2x|的圖象從左至右相交于點A、B,l2與函數y=|log2x|的圖象從左至右相交于點C、D.記線段AC和BD在x軸上的投影長度分別為a、b.當m變化時,求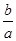 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com