中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情
在雙曲線-=1上支上有不同的三點A(x1,y1)、B(x0,6)、C(x2,y2)與焦點F（0，5）的距離成等差數列.（1）求y1+y2的值；（2）求證：線段AC的中垂線經過某一定點，并求出這個定點坐標.

思路解析：雙曲線上一點與焦點的連線問題，常考慮焦半徑比較簡單.

（1）解法一：∵BF==3,|AF|=,又∵A（x1,y1）在雙曲線上，∴x12=.∴|AF|2=x12+(y1-5)2=+(y1-5)2=(5y1-12)2,由A、B、C在雙曲線的同一支上，即上半支上.∴y1≥2,5y1-12＞0.∴AF=(5y1-12).同理可求得CF=(5y2-12),由于AF+CF=2BF,∴(5y1-12)+(5y2-12)=6.∴y1+y2=12.

解法二：∵雙曲線的實半軸長為a=2，虛半軸b=，半焦距c=5，與焦點F(0,5)對應的準線方程為y=.由雙曲線第二定義知，=,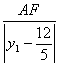

∵y1≥2,∴y1-＞0.∴|AF|=(y1-).

同理CF=·(y1-),|BF|=(6-)=3.

∵|AF|+|CF|=2|BF|,∴y1+y2=12.

解法三：雙曲線的離心率e==,|AF|=|ey1-a|=ey1-a,|CF|=|ey2-a|=ey2-a,|BF|=×6-2=3，又∵|AF|+|CF|=2|BF|=6，

∴e(y1+y2)-2a=6.∴y1+y2=12.

（2）證明：線段AC中點M(,6),kAC=,∴線段AC的垂直平分線方程為y-6=(x-)=x-.                                 ①

∵-=1,-=1,兩式相減,得x12-x22=(y12-y22),

又∵y1+y2=12,∴x12-x22=13(y1-y2).代入①,

得y-6=x+ .

∴y-=x.∴恒過點(0,).


練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

（2013•鎮江一模）設雙曲線
x2
a2
-
y2
b2
=1的左、右焦點分別為F1，F2，點P在雙曲線的右支上，且PF1=4PF2，則此雙曲線離心率的最大值為
5
3
5
3
．

查看答案和解析>>

科目：高中數學 來源： 題型：

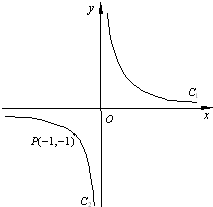設雙曲線xy=1的兩支為C1，C2（如圖），正三角形PQR的三頂點位于此雙曲線上．
（1）求證：P、Q、R不能都在雙曲線的同一支上；
（2）設P（-1，-1）在C2上，Q、R在C1上，求頂點Q、R的坐標．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知雙曲線
x2
9
-
y2
16
=1的左右焦點分別為F1，F2，定點A（1，3），點P在雙曲線的右支上運動，則|PF1|+|PA|的最小值等于
11
11
．

查看答案和解析>>

科目：高中數學 來源： 題型：

設F1，F2分別為雙曲線
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左右焦點，若在雙曲線的右支上存在一點P滿足：①△PF1F2是以PF1為底邊的等腰三角形；②直線PF1與圓x2+y2=
1
4
a2相切，則此雙曲線的離心率為
 
．

查看答案和解析>>

同步練習冊答案