兩異面直線a,b成80°角,過空間任意一點P作直線l,使其與兩直線a,b成等角50°,則這樣的直線l有 條.
【答案】
分析:根據已知中異面直線a與b所成的角為80°,設O為空間一點,過O分別作OA∥a,OB∥b,則OA,OB成80°角.過O點作出直線OA,OB相交所成角的兩條角平分線,滿足題意的直線或為兩平分線或其射影為兩平分線,由此確定直線條數.
解答:解:首先給出兩個性質①與一個角∠AOB的兩邊成等角的直線在面AOB內的射影是∠AOB的平分線.
②若∠AOC所在平面與∠BOC所在平面垂直,則有cos∠AOCcos∠BOC=cos∠AOB.
在空間任取一點O,作OA∥a,OB∥b,則OA,OB成80°角,不妨設∠AOB=80°,如圖
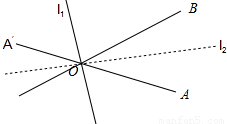
(1)直線l
1為∠AOB的補角∠A′OB=100°的平分線,此時l
1與兩直線 OA,OB成等角50°,從而l
1與兩直線a,b成等角50°,若把直線l
1繞O在垂直于面A′OB 的平面內旋轉時,設
l
1與面A′OB所成的角為θ,由性質②cosθcos50°=cos50°,θ=0°,與旋轉前l
1重合. 即此時只有一條直線滿足題意.
(2)直線l
2為∠AOB的平分線,顯然l
2與兩直線 OA,OB成等角40°,若把直線l
2繞O在垂直于面AOB 的平面內旋轉時,設l
2與面AOB所成的角為θ,由性質②cosθcos40°=cos50°,
移向得出cosθ=
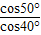
<1.存在θ,根據對稱性,在面AOB兩側各有一條.即此時共有兩條直線滿足題意.
綜上所述這樣的直線l有3條.
故答案為:3.
點評:本題考查異面直線所成的角,以及解決異面直線所成的角的方法(平移法)的應用,體現了轉化的思想和運動變化的思想方法. 本題利用定量的方法進行問題解決,當改變題干中兩個角的度數大小時,此法照樣使用.



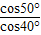 <1.存在θ,根據對稱性,在面AOB兩側各有一條.即此時共有兩條直線滿足題意.
<1.存在θ,根據對稱性,在面AOB兩側各有一條.即此時共有兩條直線滿足題意.

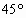 角的異面直線的對數為
角的異面直線的對數為