已知在數列{an}中,a1=1,a2n+1=qa2n-1+d(d∈R,q∈R 且q≠0,n∈N*).
(1)若數列{a2n-1}是等比數列,求q與d滿足的條件;
(2)當d=0,q=2時,一個質點在平面直角坐標系內運動,從坐標原點出發,第1次向右運動,第2次向上運動,第3次向左運動,第4次向下運動,以后依次按向右、向上、向左、向下的方向交替地運動,設第n次運動的位移是an,第n次運動后,質點到達點Pn(xn,yn),求數列{n•x4n}的前n項和Sn.
【答案】
分析:(1)根據a
1=1,a
2n+1=qa
2n-1+d(d∈R,q∈R 且q≠0,n∈N
*),若數列{a
2n-1}是等比數列,分d=0與d≠0討論解決;
(2)當d=0,q=2時,可求得
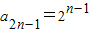
,于是x
4=a
1-a
3=1-2,
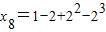
,…,從而求得x
4n=
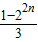
,S
n=x
4+2x
8+3x
12+…+(n-1)•x
4(n-1)+n•x
4n利用錯位相減法可求得s
n.
解答:解:(1)∵a
1=1,a
2n+1=qa
2n-1+d,q≠0,
①當d=0時,a
2n+1=qa
2n-1,顯然{a
2n-1}是等比數列;
②當d≠0時,a
3=qa
1+d=q+d,a
5=qa
3+d=q(q+d)+d.
∵數列{a
2n-1}是等比數列,
∴
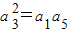
,即(q+d)
2=q(q+d)+d,化簡得q+d=1.
此時有a
2n+1=qa
2n-1+1-q,得a
2n+1-1=q(a
2n-1-1),
由 a
1=1,q≠0,得a
2n-1=1(n∈N
*),則數列{a
2n-1}是等比數列.
綜上,q與d滿足的條件為d=0(q≠0)或q+d=1(q≠0,d≠0).
(2)當d=0,q=2時,
∵a
2n+1=2a
2n-1,
∴
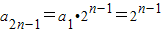
,
依題意得:x
4=a
1-a
3=1-2,
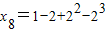
,…,
∴
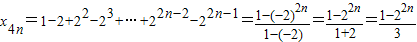
.
∴
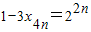
.
∴
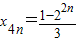
.
∴S
n=x
4+2x
8+3x
12+…+(n-1)•x
4(n-1)+n•x
4n=
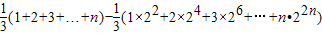
=
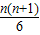
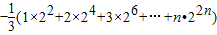
.
令
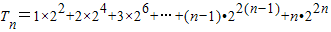
①
4T
n=1×2
4+2×2
6+3×2
8+…+(n-1)•2
2n+n•2
2n+2②
①-②得
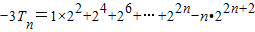
=
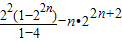
=
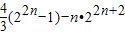
.
∴
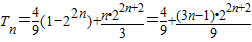
.
∴
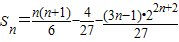
.
點評:本題考查數列遞推式,難點在于(2)x
4n的計算,著重考查數列求和,突出考查等差與等比數列的公式法求和及錯位相減法求和,屬于難題.

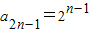 ,于是x4=a1-a3=1-2,
,于是x4=a1-a3=1-2,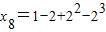 ,…,從而求得x4n=
,…,從而求得x4n=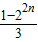 ,Sn=x4+2x8+3x12+…+(n-1)•x4(n-1)+n•x4n利用錯位相減法可求得sn.
,Sn=x4+2x8+3x12+…+(n-1)•x4(n-1)+n•x4n利用錯位相減法可求得sn.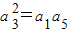 ,即(q+d)2=q(q+d)+d,化簡得q+d=1.
,即(q+d)2=q(q+d)+d,化簡得q+d=1.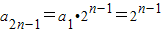 ,
,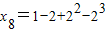 ,…,
,…,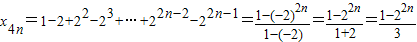 .
.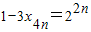 .
.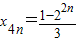 .
.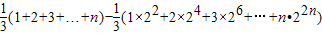 =
=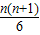
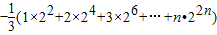 .
.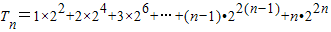 ①
①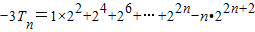 =
=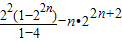 =
=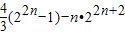 .
.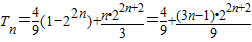 .
.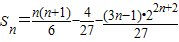 .
.

 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案