
已知某中學高三文科班學生共有800人參加了數學與地理的水平測試,現學校決定利用隨機數表法從中抽取100人進行成績抽樣調查,先將800人按001,002, ,800進行編號;
(1)如果從第8行第7列的數開始向右讀,請你依次寫出最先檢查的3個人的編號;
(下面摘取了第7行到第9行)
(2)抽取的100的數學與地理的水平測試成績如下表:
成績分為優秀、良好、及格三個等級;橫向,縱向分別表示地理成績與數學成績,例如:表中數學成績為良好的共有20+18+4=42,若在該樣本中,數學成績優秀率是30%,求a,b的值:
| 人數 | 數學 | |||
| 優秀 | 良好 | 及格 | ||
| 地理 | 優秀 | 7 | 20 | 5 |
| 良好 | 9 | 18 | 6 | |
| 及格 | a | 4 | b | |
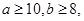 求數學成績為優秀的人數比及格的人數少的概率.
求數學成績為優秀的人數比及格的人數少的概率. (1)785,667,199(2) (3)
(3)
解析試題分析:
(1)考查的是隨機數表法,所以從第8行第7列的第一個開始數三個數構成一個三位數,該三位數必須小于或等于800,如果大于800,則舍去,繼續數直到得到三個小于或等于800的三位數,即為最先檢查的3個人的編號.
(2)根據數學成績的優秀率和總人數100可以列出關于a,b的兩個方程進而求出a,b的值.
(3)由總人數為100可以得到關于a+b=31,則可以得到a可以取的值和c可以取的值(兩者相互確定),進而得到所有的基本事件,在所有基本事件中找出滿足a<b的基本事件數,再根據古典概型的概率計算公式即可求出相應的概率.
試題解析:
(1)依題意,最先檢測的3個人的編號依次為785,667,199; 3分
(2)由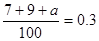 ,得
,得 , 5分
, 5分
∵ ,
,
∴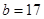 ; 7分
; 7分
(3)由題意,知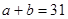 ,且
,且 ,
,
∴滿足條件的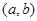 有:(10,21),(11,20),(12,19),(13,18),(14,17),(15,16),(16,15),
有:(10,21),(11,20),(12,19),(13,18),(14,17),(15,16),(16,15),
(17,14),(18,13),(19,12),(20,11),(21,10),(22,9),(23,8)共14組,
且每組出現的可能性相同. 9分
其中數學成績為優秀的人數比及格的人數少有:
(10,21),(11,20),(12,19),(13,18),(14,17),(15,16)共6組. 11分
∴數學成績為優秀的人數比及格的人數少的概率為 . 12分
. 12分
考點:隨機數表法古典概型


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
某中學高三文科班學生參加了數學與地理水平測試,學校從測試合格的學生中隨機抽取100人的成績進行統計分析.抽取的100人的數學與地理的水平測試成績如下表: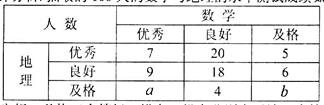
成績分為優秀、良好、及格三個等級,橫向、縱向分別表示地理成績與數學成績,例如:表中數學成績為良好的共有20+18+4=42人.
(1)若在該樣本中,數學成績優秀率為30%,求a,b的值;
(2)若樣本中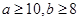 ,求在地理成績及格的學生中,數學成績優秀的人數比及格的人數少的概率.
,求在地理成績及格的學生中,數學成績優秀的人數比及格的人數少的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某中學將 名高一新生分成水平相同的甲、乙兩個“平行班”,每班
名高一新生分成水平相同的甲、乙兩個“平行班”,每班 人,吳老師采用
人,吳老師采用 、
、 兩種不同的教學方式分別在甲、乙兩個班進行教學實驗.為了解教學效果,期末考試后,分別從兩個班級中各隨機抽取
兩種不同的教學方式分別在甲、乙兩個班進行教學實驗.為了解教學效果,期末考試后,分別從兩個班級中各隨機抽取 名學生的成績進行統計,作出的莖葉圖如下:
名學生的成績進行統計,作出的莖葉圖如下:
記成績不低于 分者為“成績優秀”.
分者為“成績優秀”.
(1)在乙班樣本的 個個體中,從不低于
個個體中,從不低于 分的成績中隨機抽取
分的成績中隨機抽取 個,記隨機變量
個,記隨機變量 為抽到“成績優秀”的個數,求
為抽到“成績優秀”的個數,求 的分布列及數學期望
的分布列及數學期望 ;
;
(2)由以上統計數據填寫下面 列聯表,并判斷有多大把握認為“成績優秀”與教學方式有關?
列聯表,并判斷有多大把握認為“成績優秀”與教學方式有關?
| | 甲班( 方式) 方式) | 乙班( 方式) 方式) | 總計 |
| 成績優秀 | | | |
| 成績不優秀 | | | |
| 總計 | | | |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為調查某地區老年人是否需要志愿者提供幫助,用簡單隨機抽樣方法從該地區調查了500位老年人,結果如下:
| 性別 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
| P(K2≥x0) | 0.050 | 0.010 | 0.001 |
| x0 | 3.841 | 6.635 | 10.828 |

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
有甲、乙兩個工廠生產同一種產品,產品分為一等品和二等品.為了考察這兩個工廠的產品質量的水平是否一致,從甲、乙兩個工廠中分別隨機地抽出產品109件,191件,其中甲工廠一等品58件,二等品51件,乙工廠一等品70件,二等品121件.
(1)根據以上數據,建立2×2列聯表;
(2)試分析甲、乙兩個工廠的產品質量有無顯著差別(可靠性不低于99%).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在某大學聯盟的自主招生考試中,報考文史專業的考生參加了人文基礎學科考試科目“語文”和“數學”的考試.某考場考生的兩科考試成績數據統計如下圖所示,本次考試中成績在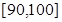 內的記為
內的記為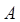 ,其中“語文”科目成績在
,其中“語文”科目成績在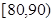 內的考生有10人.
內的考生有10人.
(1)求該考場考生數學科目成績為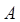 的人數;
的人數;
(2)已知參加本考場測試的考生中,恰有2人的兩科成績均為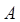 .在至少一科成績為
.在至少一科成績為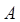 的考生中,隨機抽取2人進行訪談,求這2人的兩科成績均為
的考生中,隨機抽取2人進行訪談,求這2人的兩科成績均為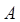 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
從某校高三上學期期末數學考試成績中,隨機抽取了 名學生的成績得到頻率分布直方圖如下:
名學生的成績得到頻率分布直方圖如下:
(1)根據頻率分布直方圖,估計該校高三學生本次數學考試的平均分;
(2)若用分層抽樣的方法從分數在 和
和 的學生中共抽取
的學生中共抽取 人,該
人,該 人中成績在
人中成績在 的有幾人?
的有幾人?
(3)在(2)中抽取的 人中,隨機抽取
人中,隨機抽取 人,求分數在
人,求分數在 和
和 各
各 人的概率.
人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某學校隨機抽取部分新生調查其上學路上所需時間(單位:分鐘),并將所得數據繪制成頻率分布直方圖(如圖),其中,上學路上所需時間的范圍是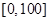 ,樣本數據分組為
,樣本數據分組為 ,
,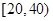 ,
,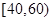 ,
,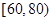 ,
,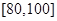 .
.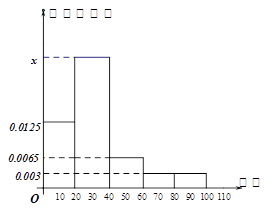
(1)求直方圖中 的值;
的值;
(2)如果上學路上所需時間不少于40分鐘的學生可申請在學校住宿,請估計學校1000名新生中有多少名學生可以申請住宿;
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某種產品特約經銷商根據以往當地的需求情況,得出如下該種產品日需求量的頻率分布直方圖.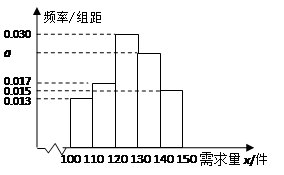
(1)求圖中 的值,并估計日需求量的眾數;
的值,并估計日需求量的眾數;
(2)某日,經銷商購進130件該種產品,根據近期市場行情,當天每售出 件能獲利30元,未售出的部分,每件虧損20元.設當天的需求量為
件能獲利30元,未售出的部分,每件虧損20元.設當天的需求量為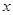 件(
件( ),純利潤為
),純利潤為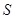 元.
元.
(ⅰ)將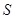 表示為
表示為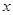 的函數;
的函數;
(ⅱ)根據直方圖估計當天純利潤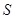 不少于
不少于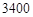 元的概率.
元的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com