
已知f(n)=1+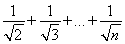 n∈N?),g(n)=2(
n∈N?),g(n)=2(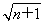 -1)(n∈N?).
-1)(n∈N?).
(1)當n=1,2,3時,分別比較f(n)與g(n)的大小(直接給出結論);
(2)由(1)猜想f(n)與g(n)的大小關系,并證明你的結論.
(1)當n=1時,f(1)>g(1);當n=2時,f(2)>g(2);當n=3時,f(3)>g(3).(2)f(n)>g(n)(n∈N*),
【解析】(1)當n=1時,f(1)>g(1);當n=2時,f(2)>g(2);當n=3時,f(3)>g(3).
(2)猜想:f(n)>g(n)(n∈N*),即1+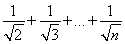 >2(
>2(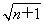 -1)(n∈N*).
-1)(n∈N*).
下面用數學歸納法證明:①當n=1時,f(1)=1,g(1)=2(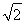 -1),f(1)>g(1).
-1),f(1)>g(1).
②假設當n=k時,猜想成立,即1+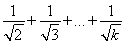 >2(
>2( -1).
-1).
則當n=k+1時,f(k+1)=1+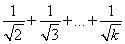 +
+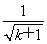 >2(
>2(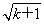 -1)+
-1)+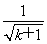 =2
=2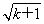 +
+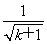 -2,而g(k+1)=2(
-2,而g(k+1)=2(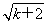 -1)=2
-1)=2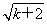 -2,
-2,
下面轉化為證明: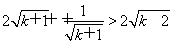 .
.
只要證:2(k+1)+1=2k+3>2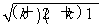 ,
,
需證:(2k+3)2>4(k+2)(k+1),即證:4k2+12k+9>4k2+12k+8,此式顯然成立.
所以,當n=k+1時猜想也成立.綜上可知:對n∈N*,猜想都成立,
即1+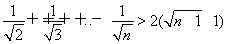 (n∈N*)成立.
(n∈N*)成立.


 考前必練系列答案
考前必練系列答案科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第三章第4課時練習卷(解析版) 題型:填空題
化簡:tan(18°-x)tan(12°+x)+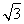 [tan(18°-x)+tan(12°+x)]=________.
[tan(18°-x)+tan(12°+x)]=________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第三章第1課時練習卷(解析版) 題型:解答題
如果點P(sinθ·cosθ,2cosθ)位于第三象限,試判斷角θ所在的象限;
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第七章第3課時練習卷(解析版) 題型:填空題
用數學歸納法證明“當n為正偶數時xn-yn能被x+y整除”第一步應驗證n=________時,命題成立;第二步歸納假設成立應寫成____.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第七章第2課時練習卷(解析版) 題型:填空題
設函數f0(x)=1-x2,f1(x)= ,fn(x)=
,fn(x)= ,(n≥1,n≥N),則方程f1(x)=
,(n≥1,n≥N),則方程f1(x)=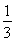 有________個實數根,方程fn(x)=
有________個實數根,方程fn(x)=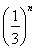 有________個實數根.
有________個實數根.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第七章第1課時練習卷(解析版) 題型:解答題
已知橢圓具有性質:若M、N是橢圓C上關于原點對稱的兩個點,點P為橢圓上任意一點,當直線PM、PN的斜率都存在,并記為kPM、kPN,那么kPM與kPN之積是與點P位置無關的定值.試對雙曲線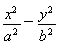 =1寫出具有類似特性的性質,并加以證明.
=1寫出具有類似特性的性質,并加以證明.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年高考數學總復習考點引領+技巧點撥第一章第1課時練習卷(解析版) 題型:填空題
已知集合A={1,2,3,4,5},B={(x,y)|x∈A,y∈A,x-y∈A},則B中元素的個數為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com