
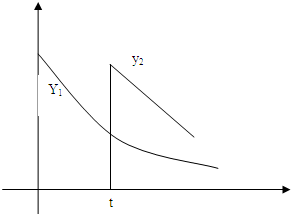 心理學家研究某位學生的學習情況發現:若這位學生剛學完的知識存留量為1,則x天后的存留量y1=
心理學家研究某位學生的學習情況發現:若這位學生剛學完的知識存留量為1,則x天后的存留量y1=| 4 |
| x+4 |
| a |
| (t+4)2 |
| a |
| (t+4)2 |
| 8 |
| t+4 |
| 4 |
| x+4 |
| a |
| (t+4)2 |
| 8 |
| t+4 |
| 4 |
| x+4 |
| a |
| (t+4)2 |
| 8 |
| t+4 |
| 4 |
| x+4 |
| -1 |
| (5+4)2 |
| 8 |
| 5+4 |
| 4 |
| x+4 |
| -(x+4) |
| 81 |
| 4 |
| x+4 |
|
| 5 |
| 9 |
| a |
| (t+4)2 |
| 8 |
| t+4 |
| 4 |
| x+4 |
| -a(x+4) |
| (t+4)2 |
| 4 |
| x+4 |
| 8 |
| t+4 |
| a(t+4) |
| (t+4)2 |
|
| 8-a |
| t+4 |
| -a(x+4) |
| (t+4)2 |
| 4 |
| x+4 |
| 2 | ||
|
| 2 | ||
|
| ab |


科目:高中數學 來源:2011-2012學年江蘇省高三下學期質量檢測數學試卷 題型:解答題
心理學家研究某位學生的學習情況發現:若這位學生剛學完的知識存留量記為1,則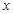 天后的存留量
天后的存留量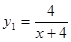 ;若在
;若在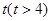 天時進行第一次復習,則此時知識存留量比未復習情況下增加一倍(復習時間忽略不計),其后存儲量
天時進行第一次復習,則此時知識存留量比未復習情況下增加一倍(復習時間忽略不計),其后存儲量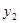 隨時間變化的曲線恰為直線的一部分,其斜率為
隨時間變化的曲線恰為直線的一部分,其斜率為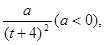 存留量隨時間變化的曲線如圖所示.當進行第一次復習后的存留量與不復習的存留量相差最大時,則稱此時此刻為“二次復習最佳時機點”.
存留量隨時間變化的曲線如圖所示.當進行第一次復習后的存留量與不復習的存留量相差最大時,則稱此時此刻為“二次復習最佳時機點”.
(1)若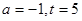 ,求“二次最佳時機點”;
,求“二次最佳時機點”;
(2)若出現了“二次復習最佳時機點”,求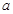 的取值范圍.
的取值范圍.
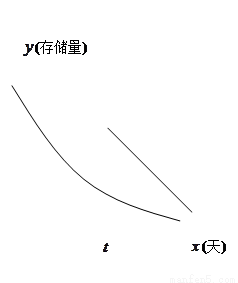
查看答案和解析>>
科目:高中數學 來源:2011年江蘇省蘇北四市高考數學二模試卷(解析版) 題型:解答題
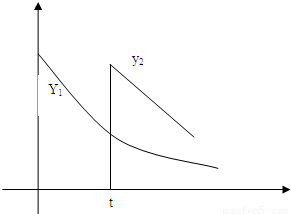 心理學家研究某位學生的學習情況發現:若這位學生剛學完的知識存留量為1,則x 天后的存留量
心理學家研究某位學生的學習情況發現:若這位學生剛學完的知識存留量為1,則x 天后的存留量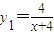 ;若在t(t>0)天時進行第一次復習,則此時這似乎存留量比未復習情況下增加一倍(復習的時間忽略不計),其后存留量y2隨時間變化的曲線恰好為直線的一部分,其斜率為
;若在t(t>0)天時進行第一次復習,則此時這似乎存留量比未復習情況下增加一倍(復習的時間忽略不計),其后存留量y2隨時間變化的曲線恰好為直線的一部分,其斜率為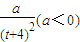 ,存留量隨時間變化的曲線如圖所示.當進行第一次復習后的存留量與不復習的存留量相差最大時,則稱此時刻為“二次復習最佳時機點”
,存留量隨時間變化的曲線如圖所示.當進行第一次復習后的存留量與不復習的存留量相差最大時,則稱此時刻為“二次復習最佳時機點”查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com