
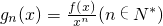 .若對定義域內的每一個x,總有gn(x)<0,則稱f(x)為“n階負函數”;若對定義域內的每一個x,總有
.若對定義域內的每一個x,總有gn(x)<0,則稱f(x)為“n階負函數”;若對定義域內的每一個x,總有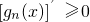 ,則稱f(x)為“n階不減函數”(
,則稱f(x)為“n階不減函數”(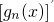 為函數gn(x)的導函數).
為函數gn(x)的導函數).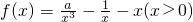 既是“1階負函數”,又是“1階不減函數”,求實數a的取值范圍;
既是“1階負函數”,又是“1階不減函數”,求實數a的取值范圍;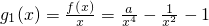 在(0,+∞)上單調遞增,
在(0,+∞)上單調遞增,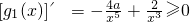 恒成立,得
恒成立,得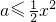 ,…(2分)
,…(2分)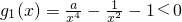 顯然在(0,+∞)恒成立,
顯然在(0,+∞)恒成立,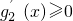 ,可得g2(x)在(0,+∞)上單調遞增,
,可得g2(x)在(0,+∞)上單調遞增,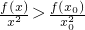 恒成立,即
恒成立,即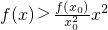 恒成立,
恒成立,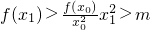 (其中m為任意常數),
(其中m為任意常數), ,即有f(x3)>0,
,即有f(x3)>0,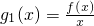 =
=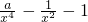 ,將[g1(x)]′≥0化簡整理,可得
,將[g1(x)]′≥0化簡整理,可得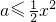 在(0,+∞)上恒成立,因此a≤0.再將a≤0代入g1(x)表達式,可得g1(x)<0在(0,+∞)上恒成立,由此可得滿足條件的實數a的取值范圍為(-∞,0];
在(0,+∞)上恒成立,因此a≤0.再將a≤0代入g1(x)表達式,可得g1(x)<0在(0,+∞)上恒成立,由此可得滿足條件的實數a的取值范圍為(-∞,0];

 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 3 | 4 |
| 3 | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com