(1)證明:∵f(xy)=f(x)+f(y),∴
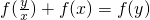
,
∴
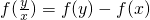
;
(2)解:∵f(x
1)<f(x
2),∴f(x
1)-f(x
2)<0,
又
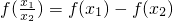
,所以
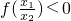
∵當且僅當x>1時,f(x)<0成立,∴當f(x)<0時,x>1,
∴

,x
1>x
2(3)解:令x=y=1代入f(xy)=f(x)+f(y)得f(1)=f(1)+f(1),f(1)=0,
∴f(x
2-2x+1)>0?f(x
2-2x+1)>f(1),
由(2)可知函數f(x)在定義域(0,+∞)上是減函數,
∴0<x
2-2x+1<1,
解得0<x<2且x≠1,
∴不等式解集為(0,1)∪(1,2)
分析:(1)取y=

,代入已知等式即可證得結果;
(2)由f(x
1)<f(x
2),結合(1)中等式
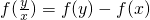
,得到
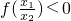
,再根據當且僅當x>1時,f(x)<0成立得到

,從而得到x
1>x
2;
(3)在已知等式中取特值x=y=1求出f(1)=0,由(2)可知函數f(x)在定義域(0,+∞)上是減函數,在不等式f(x
2-2x+1)>0中,用f(1)替換0后利用函數的單調性脫掉“f”,則不等式的解集可求.
點評:本題考查了抽象函數的應用,考查了函數的單調性的判斷與證明,訓練了特值法求函數的值,考查了學生靈活處理問題和解決問題的能力,屬中檔題.

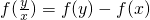 ;
;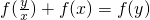 ,
,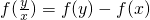 ;
;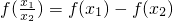 ,所以
,所以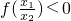
 ,x1>x2
,x1>x2 ,代入已知等式即可證得結果;
,代入已知等式即可證得結果;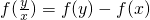 ,得到
,得到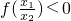 ,再根據當且僅當x>1時,f(x)<0成立得到
,再根據當且僅當x>1時,f(x)<0成立得到 ,從而得到x1>x2;
,從而得到x1>x2;

 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案