Question

已知偶函數y＝f(x)＝ax²＋bx＋c的最小值為－1，且f(1)＝0．

(1)求該函數的表達式f(x)．

(2)過曲線C：y＝f(x)(x＞0)上的點P作曲線C的切線，與x軸、y軸分別交于點M，N，試確定點P的坐標，使△MON的面積最小．

[求商的導數的法則是：＝]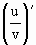

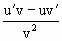Answer 1

答案：
解析：

解：(1)因為該函數為偶函數， 　　所以f(－x)＝f(x)對定義域內一切x∈R正成立．所以f(－1)＝f(1)，所以b＝0．因為f(1)＝0，所以a＋c＝0，c＝－a．所以f(x)＝ax2－a．由此，當a＞0時，f(x)有最小值－a．所以－a＝－1，a＝1，所以f(x)＝x2－1． 　　(2)如圖所示，設切點為P(u，t)，則t＝u2－1．因為y＝x2－1(x＞0)，所以＝2x，kt＝2u． 　　所以過P點的切線l的方程為y－t＝2u(x－u)．則切線l與x，y軸的交點分別為M(，0)，N(0，－u2－1)．所以△MON的面積S＝(u2＋1)＝．所以＝＝．令＝0，則u＝±．因為u＞0，所以u＝．當0＜u＜，時＜0，S遞減；當u＞時，＞0，S遞增．所以當u＝時，S有極小值，且為最小值，此時t＝u2－1＝－．所以，點P的坐標為(，－)．