
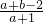 的取值范圍是________.
的取值范圍是________.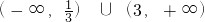
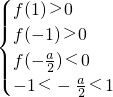 ,即
,即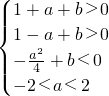 作出此不等式對應的區域,如圖中陰影部分,不包括邊界,由于
作出此不等式對應的區域,如圖中陰影部分,不包括邊界,由于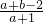 =1+
=1+ ,而
,而 可看作點P(-1,3)與陰影部分內一點(a,b)連線的斜率,由此問題轉化為線性規劃求范圍問題,易解.
可看作點P(-1,3)與陰影部分內一點(a,b)連線的斜率,由此問題轉化為線性規劃求范圍問題,易解.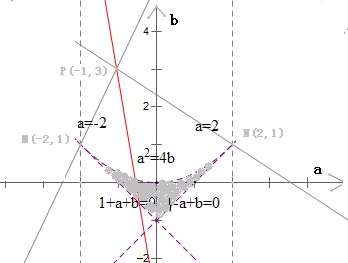 解:關于x的方程x2+ax+b=0的兩根均在區間(-1,1)內,令f(x)=x2+ax+b
解:關于x的方程x2+ax+b=0的兩根均在區間(-1,1)內,令f(x)=x2+ax+b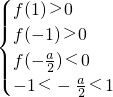 ,即
,即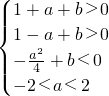 此不等式對應的區域圖象如圖陰影部分,不包括邊界.
此不等式對應的區域圖象如圖陰影部分,不包括邊界.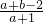 =1+
=1+ ,而
,而 可看作點
可看作點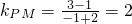 ,
,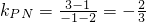 ,由圖知
,由圖知 ∈(2,+∞)∪(-∞,
∈(2,+∞)∪(-∞, )
)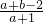 =1+
=1+ ∈
∈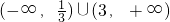
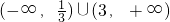
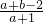 的取值范圍是解題的關鍵,由于本題通過根的分布的知識得出的不等式組較復雜,不宜將求
的取值范圍是解題的關鍵,由于本題通過根的分布的知識得出的不等式組較復雜,不宜將求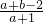 的取值范圍的問題轉化為函數的值域求解,轉化為線性規劃知識求解是本題的難點也是重點,本題考查了轉化的思想,數形結合的思想,考查轉化化歸的能力及數形結合解題的意識,綜合性強,是能力型題
的取值范圍的問題轉化為函數的值域求解,轉化為線性規劃知識求解是本題的難點也是重點,本題考查了轉化的思想,數形結合的思想,考查轉化化歸的能力及數形結合解題的意識,綜合性強,是能力型題 

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com