
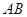 長度為
長度為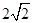 ,
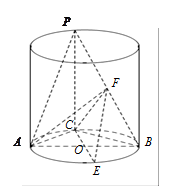
,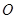 為底面圓心,正三角形
為底面圓心,正三角形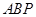 的一個頂點
的一個頂點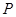 在上底面的圓周上,
在上底面的圓周上,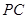 為圓柱的母線,
為圓柱的母線,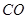 的延長線交
的延長線交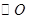 于點
于點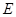 ,
, 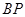 的中點為
的中點為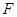 .
.
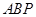 ⊥平面
⊥平面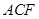 ;
;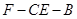 的正切值.
的正切值.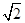 .
. 的直徑,∴
的直徑,∴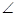 ACB=90°即 AC⊥BC ………………………………3分
ACB=90°即 AC⊥BC ………………………………3分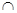 BC=C,∴AC⊥平面PBC, ………………………………………………4分
BC=C,∴AC⊥平面PBC, ………………………………………………4分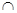 AF=A,∴PB⊥平面ACF,…………………………………………………6分
AF=A,∴PB⊥平面ACF,…………………………………………………6分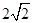 ,可證RT
,可證RT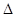 ABC≌RT
ABC≌RT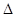 PBC,
PBC,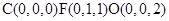 ……………………………9分
……………………………9分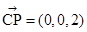 為平面CEB的一個法向量………………10分
為平面CEB的一個法向量………………10分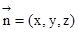 平面CEF的一個法向量,
平面CEF的一個法向量,
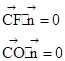 即
即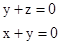 ,令y=-1則
,令y=-1則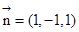 ……………………11分
……………………11分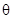 ,
, ……………………………………………12分
……………………………………………12分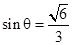 , ……………………………………………………………………13分
, ……………………………………………………………………13分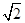 ………………………………………14分
………………………………………14分

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:不詳 題型:解答題
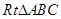 中,
中,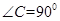 ,D,E分別為AC,AB的中點,點F為線段CD上的一點,將
,D,E分別為AC,AB的中點,點F為線段CD上的一點,將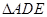 沿DE折起到
沿DE折起到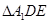 的位置,使
的位置,使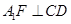 ,如圖2.
,如圖2.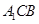
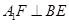
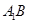 上是否存在點Q,使
上是否存在點Q,使 ?說明理由。
?說明理由。
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
 處,同一時刻,一個長
處,同一時刻,一個長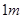 ,一端接觸地面且與地面垂直的竹竿的影子長為
,一端接觸地面且與地面垂直的竹竿的影子長為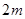 ,則該球的半徑等于( )
,則該球的半徑等于( )A.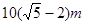 | B. | C.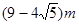 | D.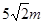 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
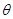 角的直線一定有無窮多條。
角的直線一定有無窮多條。查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com