
設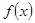 是定義在
是定義在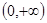 上的函數,且
上的函數,且 ,對任意
,對任意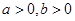 ,若經過點
,若經過點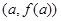 ,
,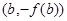 的直線與
的直線與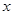 軸的交點為
軸的交點為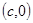 ,則稱
,則稱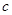 為
為 關于函數
關于函數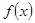 的平均數,記為
的平均數,記為 ,例如,當
,例如,當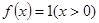 時,可得
時,可得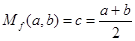 ,即
,即 為
為 的算術平均數.
的算術平均數.
當 時,
時, 為
為 的幾何平均數;
的幾何平均數;
當 時,
時, 為
為 的調和平均數
的調和平均數 ;
;
(以上兩空各只需寫出一個符合要求的函數即可)
 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:高中數學 來源: 題型:填空題
已知定義在 上的偶函數
上的偶函數 滿足:
滿足: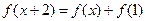 且在區間
且在區間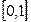 上
上
單調遞增,那么,下列關于此函數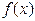 性質的表述:
性質的表述:
①函數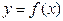 的圖象關于直線
的圖象關于直線 對稱; ②函數
對稱; ②函數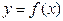 是周期函數;
是周期函數;
③當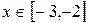 時,
時, ; ④函數
; ④函數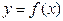 的圖象上橫坐標為偶數的點都是函數的極小值點。 其中正確表述的番號是 .
的圖象上橫坐標為偶數的點都是函數的極小值點。 其中正確表述的番號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
對于函數 ,若存在實數對(
,若存在實數對( ),使得等式
),使得等式 對定義域中的每一個
對定義域中的每一個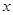 都成立,則稱函數
都成立,則稱函數 是“(
是“( )型函數”.
)型函數”.
(1) 判斷函數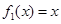 是否為 “(
是否為 “( )型函數”,并說明理由;
)型函數”,并說明理由;
(2) 若函數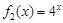 是“(
是“( )型函數”,求出滿足條件的一組實數對
)型函數”,求出滿足條件的一組實數對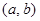 ;
;
(3)已知函數 是“
是“ 型函數”,對應的實數對
型函數”,對應的實數對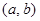 為
為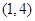 ,當
,當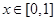 時,
時,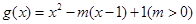 ,若當
,若當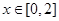 時,都有
時,都有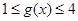 ,試求
,試求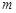 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知定義域為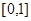 的函數
的函數 同時滿足以下三個條件:
同時滿足以下三個條件:
①對任意的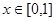 ,總有
,總有 ;
;
②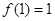 ;
;
③當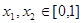 ,且
,且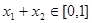 時,
時,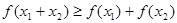 成立.
成立.
稱這樣的函數為“友誼函數”.
請解答下列各題:
(1)已知 為“友誼函數”,求
為“友誼函數”,求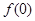 的值;
的值;
(2)函數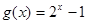 在區間
在區間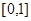 上是否為“友誼函數”?請給出理由;
上是否為“友誼函數”?請給出理由;
(3)已知 為“友誼函數”,假定存在
為“友誼函數”,假定存在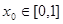 ,使得
,使得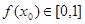 ,且
,且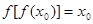 ,求證:
,求證: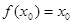 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某公司為一家制冷設備廠設計生產一種長方形薄板,其周長為4米,這種薄板須沿其對角線折疊后使用.如圖所示,ABCD(AB>AD)為長方形薄板,沿AC折疊后,AB′交DC于點P.當△ADP的面積最大時最節能,凹多邊形ACB′PD的面積最大時制冷效果最好.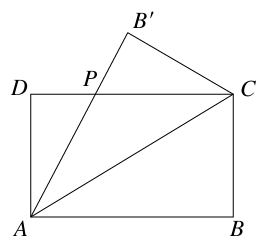
(1)設AB=x(米),用x表示圖中DP的長度,并寫出x的取值范圍;
(2)若要求最節能,應怎樣設計薄板的長和寬?
(3)若要求制冷效果最好,應怎樣設計薄板的長和寬?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com