
已知函數 , 在
, 在 處取得極小值2.
處取得極小值2.
(1)求函數 的解析式;
的解析式;
(2)求函數 的極值;
的極值;
(3)設函數 , 若對于任意
, 若對于任意 ,總存在
,總存在 , 使得
, 使得 , 求實數
, 求實數  的取值范圍.
的取值范圍.
(1)函數 的解析式為
的解析式為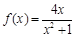 ;(2)
;(2)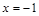 時,函數
時,函數 有極小值-2;當
有極小值-2;當 時,函數
時,函數 有極大值2 ;(3)a的取值范圍是(-∞,-1]∪[ 3,+∞).
有極大值2 ;(3)a的取值范圍是(-∞,-1]∪[ 3,+∞).
解析試題分析:(1)根據函數在極值處導函數為0,極小值為2聯立方程組即可求得m,n;(2)由(1)求得函數解析式,對函數求導且讓導函數為0,即可求得極大值和極小值;(3)依題意只需
科目:高中數學
來源:
題型:解答題
甲方是一農場,乙方是一工廠.由于乙方生產需占用甲方的資源,因此甲方有權向乙方索賠以彌補經濟損失并獲得一定凈收入,在乙方不賠付甲方的情況下,乙方的年利潤x(元)與年產量t(噸)滿足函數關系x=2 000
科目:高中數學
來源:
題型:解答題
已知函數
科目:高中數學
來源:
題型:解答題
如圖,現要在邊長為
科目:高中數學
來源:
題型:解答題
已知函數f(x)=
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區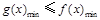 即可,當
即可,當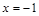 時,函數
時,函數 有最小值-2 ,即對任意
有最小值-2 ,即對任意 總存在
總存在 ,使得
,使得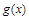 的最小值不大于-2 ;而
的最小值不大于-2 ;而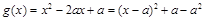 ,分
,分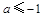 、
、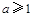 、
、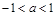 三種情況討論即可.
三種情況討論即可.
試題解析:(1)∵函數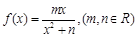 在
在 處取得極小值2,∴
處取得極小值2,∴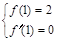 1分
1分
又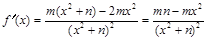 ∴
∴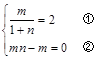
由②式得m=0或n=1,但m=0顯然不合題意 ∴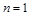 ,代入①式得m=4
,代入①式得m=4
∴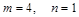 2分
2分
經檢驗,當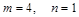 時,函數
時,函數 在
在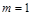 處取得極小值2
處取得極小值2
∴函數 的解析式為
的解析式為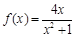 4分
4分
(2)∵函數 的定義域為
的定義域為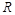 且由(1)有
且由(1)有 
令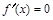 ,解得:
,解得: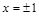
∴當x變化時,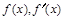 的變化情況如下表:
的變化情況如下表:x (-∞,-1) -1 (-1,1) 1 (1,+∞) 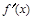
— 0 + 0 — 
減 極小值-2


模擬試卷匯編優化系列答案
學期總復習期末復習寒假作業系列答案
贏在課堂中考先鋒總復習卷系列答案
中考風向標全國中考試題精析系列答案
宏翔教育中考金牌中考總復習系列答案
贏在中考3年中考2年模擬系列答案
宏翔文化中考亮劍系列答案
5年中考江蘇13大市中考真題歷年回顧精選28套卷系列答案
薪火文化假期百分百系列答案
定位中考三步定位核心大考卷系列答案
 .若乙方每生產一噸產品必須賠付甲方S元(以下稱S為賠付價格).
.若乙方每生產一噸產品必須賠付甲方S元(以下稱S為賠付價格).
(1)將乙方的年利潤w(元)表示為年產量t(噸)的函數,并求出乙方獲得最大利潤的年產量;
(2)甲方每年受乙方生產影響的經濟損失金額y=0.002t2(元),在乙方按照獲得最大利潤的產量進行生產的前提下,甲方要在索賠中獲得最大凈收入,應向乙方要求的賠付價格S是多少? ,其中
,其中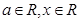 .
.
(1)當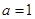 時,求函數
時,求函數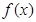 在
在 處的切線方程;
處的切線方程;
(2)若函數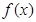 在區間(1,2)上不是單調函數,試求
在區間(1,2)上不是單調函數,試求 的取值范圍;
的取值范圍;
(3)已知 ,如果存在
,如果存在 ,使得函數
,使得函數
 在
在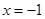 處取得最小值,試求
處取得最小值,試求 的最大值.
的最大值. 的正方形
的正方形 內建一個交通“環島”.正方形的四個頂點為圓心在四個角分別建半徑為
內建一個交通“環島”.正方形的四個頂點為圓心在四個角分別建半徑為 (
( 不小于
不小于 )的扇形花壇,以正方形的中心為圓心建一個半徑為
)的扇形花壇,以正方形的中心為圓心建一個半徑為 的圓形草地.為了保證道路暢通,島口寬不小于
的圓形草地.為了保證道路暢通,島口寬不小于 ,繞島行駛的路寬均不小于
,繞島行駛的路寬均不小于 .
.
(1)求 的取值范圍;(運算中
的取值范圍;(運算中 取
取 )
)
(2)若中間草地的造價為 元
元 ,四個花壇的造價為
,四個花壇的造價為 元
元 ,其余區域的造價為
,其余區域的造價為 元
元 ,當
,當 取何值時,可使“環島”的整體造價最低?
取何值時,可使“環島”的整體造價最低? 在x=0,x=
在x=0,x= 處存在極值。
處存在極值。
(Ⅰ)求實數a,b的值;
(Ⅱ)函數y=f(x)的圖象上存在兩點A,B使得△AOB是以坐標原點O為直角頂點的直角三角形,且斜邊AB的中點在y軸上,求實數c的取值范圍;
(Ⅲ)當c=e時,討論關于x的方程f(x)=kx(k∈R)的實根個數。
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號