
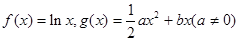 .
.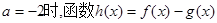 在其定義域內是增函數,求b的取值范圍;
在其定義域內是增函數,求b的取值范圍;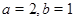 ,若函數
,若函數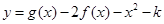 在 [1,3]上恰有兩個不同零點,求實數
在 [1,3]上恰有兩個不同零點,求實數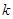 的取值范圍.
的取值范圍.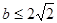 ;(2)2-2ln2<k
;(2)2-2ln2<k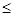 3-2ln3
3-2ln3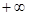 )內是增函數,可得
)內是增函數,可得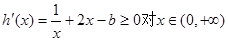 恒成立,從而通過分離參數轉化為求函數的最小值處理.
恒成立,從而通過分離參數轉化為求函數的最小值處理.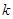
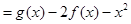 在[1,3]上恰有兩個不同的零點等價于方程
在[1,3]上恰有兩個不同的零點等價于方程 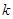 =
=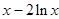 ,在[1,3]上恰有兩個相異實根; 等價于函數
,在[1,3]上恰有兩個相異實根; 等價于函數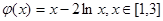 的圖象與直線
的圖象與直線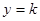 有兩個不同的交點,利用函數的導數求出函數
有兩個不同的交點,利用函數的導數求出函數 的單調區間與極值,就可畫出
的單調區間與極值,就可畫出 的大致圖象,通過圖象觀查可知
的大致圖象,通過圖象觀查可知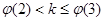 從而求得k的取值范圍.
從而求得k的取值范圍.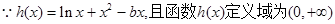 ,則:
,則: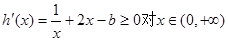 恒成立,
恒成立, 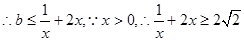 ,
,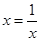 時,即
時,即 時,取等號),
時,取等號),
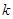
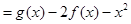 在[1,3]上恰有兩個不同的零點等價于方程
在[1,3]上恰有兩個不同的零點等價于方程 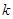 =
=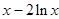 ,在[1,3]上恰有兩個相異實根.
,在[1,3]上恰有兩個相異實根.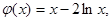 則
則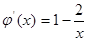 ;當
;當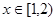 ,
,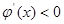 ;當
;當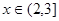 時,
時,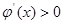 ;所以
;所以 在[1,2]上是單調遞減函數,在(2,3]上是單調遞增函數;故
在[1,2]上是單調遞減函數,在(2,3]上是單調遞增函數;故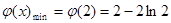 ,又
,又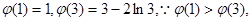 如圖故只需
如圖故只需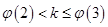 ,所以有:2-2ln2<k
,所以有:2-2ln2<k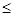 3-2ln3
3-2ln3


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com