
為了解某市今年初二年級男生的身體素質狀況,從該市初二年級男生中抽取了一部分學生進行“擲實心球”的項目測試.成績低于6米為不合格,成績在6至8米(含6米不含8米)的為及格,成績在8米至12米(含8米和12米,假定該市初二學生擲實心球均不超過12米)為優秀.把獲得的所有數據,分成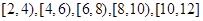 五組,畫出的頻率分布直方圖如圖所示.已知有4名學生的成績在10米到12米之間.
五組,畫出的頻率分布直方圖如圖所示.已知有4名學生的成績在10米到12米之間.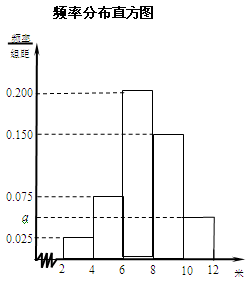
(Ⅰ)求實數 的值及參加“擲實心球”項目測試的人數;
的值及參加“擲實心球”項目測試的人數;
(Ⅱ)根據此次測試成績的結果,試估計從該市初二年級男生中任意選取一人,“擲實心球”成績為優秀的概率;
(Ⅲ)若從此次測試成績不合格的男生中隨機抽取2名學生再進行其它項目的測試,求所抽取的2名學生來自不同組的概率.
(Ⅰ)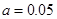 ,參加“擲實心球”的項目測試的人數為40人;(Ⅱ)成績為優秀的概率為
,參加“擲實心球”的項目測試的人數為40人;(Ⅱ)成績為優秀的概率為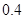 ;(Ⅲ)
;(Ⅲ)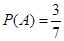
解析試題分析:(Ⅰ)有頻率分布直方圖可知,所有面積之和等于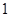 ,由此可求出
,由此可求出 ,有頻率的求法,可計算出總人數,值得注意的是:頻率分布直方圖用面積表示頻率,而不是用組高;(Ⅱ)有頻率與概率之間的關系,可估計從該市初二年級男生中任意選取一人,“擲實心球”成績為優秀的概率;(Ⅲ)分別求出不合格的各組人數,有古典概型的概率求法,寫出總的抽去方法數,找出符合條件的方法數,從而求出概率.
,有頻率的求法,可計算出總人數,值得注意的是:頻率分布直方圖用面積表示頻率,而不是用組高;(Ⅱ)有頻率與概率之間的關系,可估計從該市初二年級男生中任意選取一人,“擲實心球”成績為優秀的概率;(Ⅲ)分別求出不合格的各組人數,有古典概型的概率求法,寫出總的抽去方法數,找出符合條件的方法數,從而求出概率.
試題解析:(Ⅰ)由題意可知 ,解得
,解得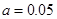 .所以此次測試總人數為
.所以此次測試總人數為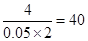 . 所以此次參加“擲實心球”的項目測試的人數為40人.
. 所以此次參加“擲實心球”的項目測試的人數為40人.
(Ⅱ)由圖可知,參加此次“擲實心球”的項目測試的初二男生,成績優秀的頻率為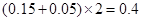 ,則估計從該市初二年級男生中任意選取一人,“擲實心球”成績為優秀的概率為
,則估計從該市初二年級男生中任意選取一人,“擲實心球”成績為優秀的概率為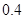 .
.
(Ⅲ)設事件A:從此次測試成績不合格的男生中隨機抽取2名學生來自不同組.由已知,測試成績在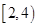 有2人,記為
有2人,記為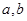 ;在
;在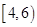 有6人,記為
有6人,記為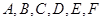 . 從這8人中隨機抽取2人有
. 從這8人中隨機抽取2人有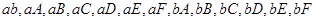 ,
, 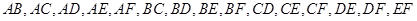 共28種情況.
共28種情況.
事件A包括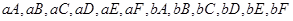 共12種情況. 所以
共12種情況. 所以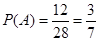 .
.
答:隨機抽取的2名學生來自不同組的概率為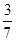 .
.
考點:頻率分布直方圖,古典概型,考查學生的運算能力.


科目:高中數學 來源: 題型:解答題
某工廠有25周歲以上(含2S周歲)工人300名,25周歲以下工人200名為研究工人的日平均生產量是否與年齡有關,現采用分層抽樣的方法,從中抽取了100名工人,先統計了他們某月的日平均生產件數,然后按工人年齡在“25周歲以上(含25周歲)”和“25周歲以下”分為兩組,再將兩組工人的日平均生產件數分成5組:[50,60),[60,70),[70,80),[80,90),[90,100),分別加以統計,得到如圖所示的頻率分布直方圖。

(1)求樣本中“25周歲以上(含25周歲)組”抽取的人數、日生產量平均數;
(2)若“25周歲以上組”中日平均生產90件及90件以上的稱為“生產能手”;“25周歲以下組”中日平均生產不足60件的稱為“菜鳥”。從樣本中的“生產能手”和”菜鳥”中任意抽取2人,求這2人日平均生產件數之和X的分布列及期望。(“生產能手”日平均生產件數視為95件,“菜鳥”日平均生產件數視為55件)。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某社團組織 名志愿者利用周末和節假日參加社會公益活動,活動內容是:1.到各社區宣傳慰問,倡導文明新風;2.到指定的醫院、福利院做義工,幫助那些需要幫助的人.各位志愿者根據各自的實際情況,選擇了不同的活動項目,相關的數據如下表所示:
名志愿者利用周末和節假日參加社會公益活動,活動內容是:1.到各社區宣傳慰問,倡導文明新風;2.到指定的醫院、福利院做義工,幫助那些需要幫助的人.各位志愿者根據各自的實際情況,選擇了不同的活動項目,相關的數據如下表所示:
| | 宣傳慰問 | 義工 | 總計 |
 歲至 歲至 歲 歲 |  |  |  |
大于 歲 歲 |  | 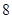 | 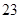 |
| 總計 |  |  |  |
 名,年齡大于
名,年齡大于 歲的應該抽取幾名?
歲的應該抽取幾名? 名志愿者中任取
名志愿者中任取 名,求選到的志愿者年齡大于
名,求選到的志愿者年齡大于 歲的人數的數學期望.
歲的人數的數學期望.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
口袋中有n(n∈N*)個白球,3個紅球.依次從口袋中任取一球,如果取到紅球,那么繼續取球,且取出的紅球不放回;如果取到白球,就停止取球.記取球的次數為X,若P(X=2)=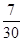 求:
求:
(1)n的值;
(2)X的概率分布與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
從某學校高三年級男生隨機抽取若干名測量身高,發現測量數據全部介于155cm和195cm之間且每個男生被抽取到的概率為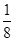 ,將測量結果按如下方式分成八組:第一組[155,160),第二組[160,165),┅,第八組[190,195),右圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組的頻數均為4,第六組,第七組,第八組的頻率依次構成等差數列。
,將測量結果按如下方式分成八組:第一組[155,160),第二組[160,165),┅,第八組[190,195),右圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組的頻數均為4,第六組,第七組,第八組的頻率依次構成等差數列。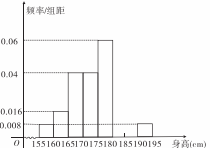
(I)補充完整頻率分布直方圖,并估計該校高三年級全體男生身高不低于180cm的人數;
(II)從最后三組中任取2名學生參加學校籃球隊,求他們來自不同組的事件概率。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某數學老師對本校2013屆高三學生的高考數學成績按1:200進行分層抽樣抽取了20名學生的成績,并用莖葉圖記錄分數如圖所示,但部分數據不小心丟失,同時得到如下所示的頻率分布表:
| 分數段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 總計 |
| 頻數 | | | | b | | |
| 頻率 | a | 0.25 | | | | |

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
從某校高三上學期期末數學考試成績中,隨機抽取了60名學生的成績得到頻率分布直方圖如下: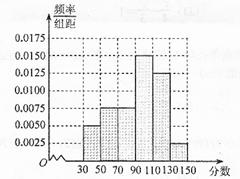
(Ⅰ)根據頻率分布直方圖,估計該校高三學生本次數學考試的平均分;
(Ⅱ)若用分層抽樣的方法從分數在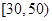 和
和 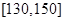 的學生中共抽取3人,該3人中成績在
的學生中共抽取3人,該3人中成績在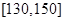 的有幾人?
的有幾人?
(Ⅲ)在(Ⅱ)中抽取的3人中,隨機抽取2人,求分數在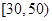 和
和 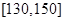 各1人的概率.
各1人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校高三有甲、乙兩個班,在某次數學測試中,每班各抽取5份試卷,所抽取的平均得分相等(測試滿分為100分),成績統計用莖葉圖表示如下:
| 甲 | | 乙 |
| 9 8 | 8 | 4 8 9 |
| 2 1 0 | 9 |  6 6 |
 ;
;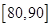 之間的概率.
之間的概率.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了解某班學生喜愛打籃球是否與性別有關,對本班50人進行了問卷調查得到了如下的列聯表:
| | 喜愛打籃球 | 不喜愛打籃球 | 合計 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合計 | | | 50 |
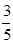 .
.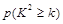 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005] | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
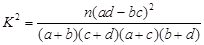 ,其中
,其中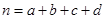 )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com