
在△ABC中,角A,B,C的對邊分別為a,b,c.已知2cos(B-C)+1=4cosBcosC.
(Ⅰ)求A;
(Ⅱ)若a=2 ,△ABC的面積為2
,△ABC的面積為2 ,求b+c.
,求b+c.
(Ⅰ)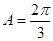 ;(Ⅱ)6.
;(Ⅱ)6.
解析試題分析:(Ⅰ) 對于2cos(B-C)+1=4cosBcosC通過三角恒等變換,再結(jié)合角的范圍即可得;(Ⅱ)利用余弦定理、面積公式可求.
試題解析:(Ⅰ) 由2cos(B-C)+1=4cosBcosC,得
2(cosBcosC+sinBsinC)+1=4cosBcosC,
即2(cosBcosC-sinBsinC)=1,亦即2cos(B+C)=1,
∴cos(B+C)= . ∵0<B+C<π,∴B+C=
. ∵0<B+C<π,∴B+C=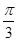 .
.
∵A+B+C=π, ∴A=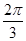 . 6分
. 6分
(Ⅱ)由(Ⅰ),得A=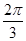 .
.
由S△ABC=2 ,得
,得 bcsin
bcsin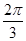 =2
=2 ,∴bc=8. ①
,∴bc=8. ①
由余弦定理a2=b2+c2-2bccosA,得
(2 )2=b2+c2-2bccos
)2=b2+c2-2bccos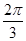 ,即b2+c2+bc=28,
,即b2+c2+bc=28,
∴(b+c)2-bc=28. ②
將①代入②,得(b+c)2-8=28,
∴b+c=6. 12分
考點:解三角形,正、余弦定理,面積公式


 探究與鞏固河南科學(xué)技術(shù)出版社系列答案
探究與鞏固河南科學(xué)技術(shù)出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
懷化市某棚戶區(qū)改造工程規(guī)劃用地近似為圖中半徑為 的圓面,圖中圓內(nèi)接四邊形
的圓面,圖中圓內(nèi)接四邊形 為擬定拆遷的棚戶區(qū),測得
為擬定拆遷的棚戶區(qū),測得 百米,
百米, 百米,
百米, 百米.
百米.
(Ⅰ)請計算原棚戶區(qū) 的面積及圓面的半徑
的面積及圓面的半徑 ;
;
(Ⅱ)因地理條件的限制,邊界 ,
, 不能變更,而邊界
不能變更,而邊界 ,
, 可以調(diào)整,為了提高棚戶區(qū)改造建設(shè)用地的利用率,請在圓弧
可以調(diào)整,為了提高棚戶區(qū)改造建設(shè)用地的利用率,請在圓弧 上求出一點
上求出一點 ,使得棚戶區(qū)改造的新建筑用地
,使得棚戶區(qū)改造的新建筑用地 的面積最大,并求最大值.
的面積最大,并求最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知 外接圓
外接圓 的半徑為
的半徑為 ,且
,且 .
.
(Ⅰ)求 邊的長及角
邊的長及角 的大小;
的大小;
(Ⅱ)從圓 內(nèi)隨機取一個點
內(nèi)隨機取一個點 ,若點
,若點 取自
取自 內(nèi)的概率恰為
內(nèi)的概率恰為 ,試判斷
,試判斷 的形狀.
的形狀.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com