
已知 是定義域?yàn)镽的奇函數(shù),
是定義域?yàn)镽的奇函數(shù),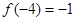 ,
, 的導(dǎo)函數(shù)
的導(dǎo)函數(shù)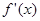 的圖象如圖所示。若兩正數(shù)
的圖象如圖所示。若兩正數(shù) 滿足
滿足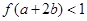 ,則
,則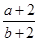 的取值范圍是
的取值范圍是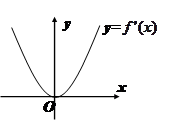
A.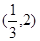 | B.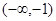 | C. | D.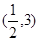 |
D
解析試題分析:先由導(dǎo)函數(shù)f′(x)是過(guò)原點(diǎn)的二次函數(shù)入手,再結(jié)合f(x)是定義域?yàn)镽的奇函數(shù)求出f(x);然后根據(jù)a、b的約束條件畫出可行域,最后利用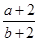 的幾何意義解決問(wèn)題.解:由f(x)的導(dǎo)函數(shù)f’(x)的圖象,設(shè)f’(x)=mx2,則f(x)=
的幾何意義解決問(wèn)題.解:由f(x)的導(dǎo)函數(shù)f’(x)的圖象,設(shè)f’(x)=mx2,則f(x)=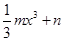 ,∵f(x)是定義域?yàn)镽的奇函數(shù),∴f(0)=0,即n=0,又f(-4)=
,∵f(x)是定義域?yàn)镽的奇函數(shù),∴f(0)=0,即n=0,又f(-4)=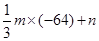 =-1,∴f(x)=
=-1,∴f(x)=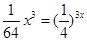
且f(a+2b)=( ,又a>0,b>0,則畫出點(diǎn)(b,a)的可行域如下圖所示
,又a>0,b>0,則畫出點(diǎn)(b,a)的可行域如下圖所示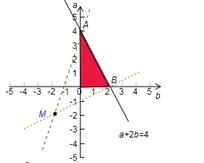
而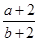 可視為可行域內(nèi)的點(diǎn)(b,a)與點(diǎn)M(-2,-2)連線的斜率.又因?yàn)閗AM=3,kBM=
可視為可行域內(nèi)的點(diǎn)(b,a)與點(diǎn)M(-2,-2)連線的斜率.又因?yàn)閗AM=3,kBM=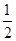
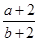 的取值范圍是
的取值范圍是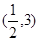 ,選D.
,選D.
考點(diǎn):斜率的幾何意義
點(diǎn)評(píng):數(shù)形結(jié)合是數(shù)學(xué)的基本思想方法:遇到二元一次不定式組要考慮線性規(guī)劃,遇到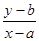 的代數(shù)式要考慮點(diǎn)(x,y)與點(diǎn)(a,b)連線的斜率.這都是由數(shù)到形的轉(zhuǎn)化策略
的代數(shù)式要考慮點(diǎn)(x,y)與點(diǎn)(a,b)連線的斜率.這都是由數(shù)到形的轉(zhuǎn)化策略



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:單選題
.設(shè)三次函數(shù) 的導(dǎo)函數(shù)為
的導(dǎo)函數(shù)為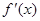 ,函數(shù)
,函數(shù)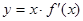 的圖象的一部分如圖所示,則正確的是
的圖象的一部分如圖所示,則正確的是 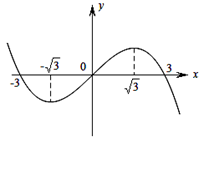
A. 的極大值為 的極大值為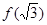 ,極小值為 ,極小值為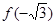 |
B. 的極大值為 的極大值為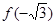 ,極小值為 ,極小值為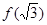 |
C. 的極大值為 的極大值為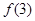 ,極小值為 ,極小值為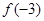 |
D. 的極大值為 的極大值為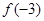 ,極小值為 ,極小值為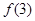 |
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com