
 ;(2)f(x)的單調遞增區間是(kπ-
;(2)f(x)的單調遞增區間是(kπ-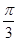 ,kπ+),k∈Z;f(x)的單調遞減區間是(kπ+,kπ+
,kπ+),k∈Z;f(x)的單調遞減區間是(kπ+,kπ+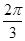 ),k∈Z;函數f(x)的對稱軸為
),k∈Z;函數f(x)的對稱軸為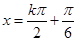 ,k∈Z;函數f(x)的對稱中心為
,k∈Z;函數f(x)的對稱中心為 ,k∈Z .
,k∈Z .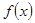 的解析式,化為標準式,然后利用周期公式
的解析式,化為標準式,然后利用周期公式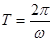 來求;(2) 根據正弦曲線的單調區間:
來求;(2) 根據正弦曲線的單調區間: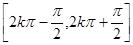 單調遞增,
單調遞增,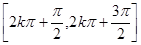 單調遞減求目標函數的單調區間,對稱軸是根據
單調遞減求目標函數的單調區間,對稱軸是根據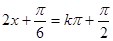 來求;對稱中心是根據
來求;對稱中心是根據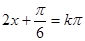 來求.
來求.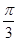 ,kπ+),k∈Z, 8分
,kπ+),k∈Z, 8分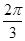 ),k∈Z. 10分
),k∈Z. 10分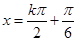 ,k∈Z, 12分
,k∈Z, 12分 ,k∈Z 14分
,k∈Z 14分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com