在平面直角坐標系
中，以
為極點，
軸非負半軸為極軸建立坐標系，已知曲線
的極坐標方程為
，直線
的參數方程為: 
（
為參數），兩曲線相交于
兩點. 求：
（1）寫出曲線的直角坐標方程和直線的普通方程；
（2）若
求
的值.
（1）
，
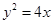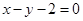；（2）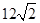
解析試題分析：（1）將曲線C的方程兩邊分別乘以
，再利用極坐標與直角坐標互化公式即可將極坐標方程化為直角坐標方程，對直線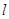
方程，消去參數t,即可化為普通方程；（2）將直線的參數方程代入曲線C的直角坐標方程，化為關于t二次方程，利用根與系數關系及參數t的幾何意義，即可求出|PM|+|PN|的值.
試題解析：(1)曲線C的直角坐標方程為，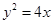
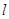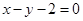直線的普通方程. 6分
(2)直線的參數方程為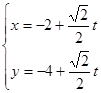
(t為參數),
代入y2=4x, 得到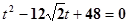
,設M,N對應的參數分別為t1,t2
則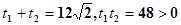
所以|PM|+|PN|=|t1+t2|=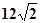
14分
考點：直角坐標方程與參數方程的互化；極坐標方程與直角坐標方程互化；直線的參數方程中參數的意義；直線與拋物線的位置關系.
科目：高中數學 來源： 題型：解答題
在直角坐標系xOy中，直線l的方程為x﹣y+4=0，曲線C的參數方程為
（α為參數）已知在極坐標（與直角坐標系xOy取相同的長度單位，且以原點O為極點，以x軸正半軸為極軸）中，點P的極坐標為（4，
），判斷點P與直線l的位置關系；
（2）設點Q是曲線C上的一個動點，求它到直線l的距離的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
曲線C的極坐標方程為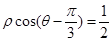
，以極點O為原點，極軸Ox為x的非負半軸，保持單位長度不變建立直角坐標系xoy.
（1）求曲線C的直角坐標方程；
（2）直線l的參數方程為
．若C與
的交點為P，求點P與點A（-2,0）的距離|PA|.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
在直角坐標系xoy中，以坐標原點為極點，x軸為極軸建立極坐標系，半圓C的極坐標方程為
，
.
（1）求C的參數方程；
（2）設點D在C上，C在D處的切線與直線
垂直，根據（1）中你得到的參數方程，確定D的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
在平面直角坐標系xOy中，以O為極點，x軸正半軸為極軸建立極坐標系，曲線C的極坐V標方程為
，M，N分別為曲線C與x軸、y軸的交點．
（1）寫出曲線C的直角坐標方程，并求M，N的極坐標；
（2）求直線OM的極坐標方程．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
在直角坐標系xOy中，直線l的方程為x－y＋2＝0，
曲線C的參數方程為
(α為參數)．
（1）已知在極坐標系(與直角坐標系xOy取相同的長度單位，且以原點O為極點，以x軸正半軸為極軸)中，點P的極坐標為
，判斷點P與直線l的位置關系；
（2）設點Q是曲線C上的一個動點，求它到直線l的距離的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
以直角坐標系的原點為極點O，
軸正半軸為極軸，已知點P的直角坐標為(1,-5),點C的極坐標為
,若直線l經過點P,且傾斜角為
，圓C的半徑為4.
(1).求直線l的參數方程及圓C的極坐標方程;
(2).試判斷直線l與圓C有位置關系.
查看答案和解析>>
科目：高中數學 來源： 題型：填空題
(坐標系與參數方程選做題)設直線
的參數方程為
（
為參數），以坐標原點為極點，x軸為極軸建立極坐標系得另一直線
的方程為
，
若直線與間的距離為
，則實數
的值為 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的極坐標方程為
，寫出曲線