
�ٌ�������x�ʣ�0,1��,����f(x)��3,��f(1)=4;
����x1��0,x2��0,x1+x2��1,�t��f(x1+x2)��f(x1)+f(x2)-3.
(1)��f(0)��ֵ;
(2)���C:f(x)��4;
(3)��x��(![]() ��(n=1,2,3,��)�r,ԇ�C��f(x)��3x+3.
��(n=1,2,3,��)�r,ԇ�C��f(x)��3x+3.
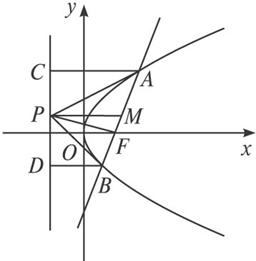
(��)��D,�O(sh��)���タy2=2px(p��0)�Ľ��c��F,��(j��ng)�^�cF��ֱ�������タ��A��B���c,��A��B���c���˞�(x1,y1)��(x2,y2),y1��0,y2��0,P�Ǵ˒��タ�Ĝʾ��ϵ�һ�c,O������ԭ�c.

(1)���C:y1y2=-p2;
(2)ֱ��PA��PF��PB�ķ���������(1,a)��(1,b)��(1,c),���C:����(sh��)a��b��c�ɵȲ(sh��)��;
(3)��![]() =0,��APF=��,��BPF=��,��PFO=��,���C:��=|��-��|.
=0,��APF=��,��BPF=��,��PFO=��,���C:��=|��-��|.
(1)��:��x1=x2=0,
�ɢٌ�������x�ʣ�0,1��,����f(x)��3,
��f(0)��3.
���ɢڵ�f(0)��2f(0)-3,
��f(0)��3;
��f(0)=3.
(2)�C��:��ȡx1��x2�ʣ�0,1��,���O(sh��)x1��x2,
�tf(x2)=f��x1+(x2-x1)�ݡ�f(x1)+f(x2-x1)-3,
��0��x2-x1��1,��f(x2-x1)��3,
��f(x2-x1)-3��0.
��f(x1)��f(x2).
�ஔx�ʣ�0,1�ݕr,f(x)��f(1)=4.
(3)�C��:����(sh��)�W�w�{���C��
f(![]() )��
)��![]() +3(n��N*).
+3(n��N*).
(1)��n=1�r,f(![]() )=f(1)=4=1+3=
)=f(1)=4=1+3=![]() +3,����ʽ����;
+3,����ʽ����;
(2)���O(sh��)��n=k�r,f(![]() )��
)��![]() +3(k��N*),
+3(k��N*),
��f(![]() )=f��
)=f��![]() +(
+(![]() +
+![]() )��
)��
��f(![]() )+f(
)+f(![]() +
+![]() )-3
)-3
��f(![]() )+f(
)+f(![]() )+f(
)+f(![]() )-6
)-6
��3f(![]() )��f(
)��f(![]() )+6��
)+6��![]() +9.
+9.
��f(![]() )��
)��![]() +3,
+3,
����n=k+1�r,����ʽ����.
��(1)(2),��֪����ʽf(![]() )��
)��![]() +3��һ��������(sh��)������.
+3��һ��������(sh��)������.
����,��x��(![]() ,
,![]() ��(n=1,2,3,��)�r,3x+3��3��
��(n=1,2,3,��)�r,3x+3��3��![]() +3=
+3=![]() +3��f(
+3��f(![]() ),
),
��x�ʣ�0,1��,f(x)���{(di��o)�f��,
��f(![]() )��f(
)��f(![]() ).
).
��f(x)��f(![]() )��3x+3.
)��3x+3.
(��)�C��:(1)�ٮ�ֱ��AB��б�ʲ����ڕr,�O(sh��)ֱ��AB�ķ��̞�x=![]() ,�tA(
,�tA(![]() ,p),B(
,p),B(![]() ,-p),
,-p),
��y1y2=-p2.
�ڮ�ֱ��AB��б�ʴ����Ҳ���0�r,�O(sh��)ֱ��AB�ķ��̞�y=k(x![]() ),
),
�t��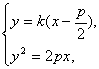 �ɵ�ky2-2py-kp2=0(k��0).��y1y2=-p2.
�ɵ�ky2-2py-kp2=0(k��0).��y1y2=-p2.
(2)����֪a=kPA,b=kPF,c=kPB,
�O(sh��)P(![]() ,t),F(
,t),F(![]() ,0),
,0),
��a=![]() ,b=
,b=![]() ,c=
,c=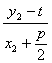 ;
;
��x1=![]() ,x2=
,x2=![]() .
.
��a+c=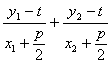
=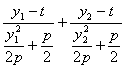
![]()
=![]()
=![]()
=![]() .
.
��a��b��c�ɵȲ(sh��)��.
(3)�C��һ:��![]() =0,
=0,
��PA��PB,��a��c=-1.
��(2)��֪a+c=2b,��a-b=b-c.
����AB��x�S,�t��=��=45��,��=0��,
���=��-��.
����kAB��0,�t
tan��=![]() .
.
ͬ���ɵ�tan��=a,
��tan(��-��)=![]() ,
,
��|tan(��-��)|=|b|=tan��.
��֪��PFO����BPF����APF�����J��.
���=|��-��|.
����kAB��0,��Ƶ�,Ҳ���C����=|��-��|.
�C������,��=|��-��|.
�C����:��![]() =0,��PA��PB.
=0,��PA��PB.
��a��c=-1.
����D,��AB��x�S,�t��=��=45��,��=0��,
���=��-��.

����kAB��0,��A��B�ڒ��タ��,
��|AF|=|AC|,|BF|=|BD|.
�O(sh��)AB���c��M,�t
|PM|=![]() ,
,
��PM������ABDC�����,
��P��CD���c.
��P(![]() ),t=
),t=![]() ,
,
F(![]() ,0),
,0),
![]() =(p,
=(p,![]() ),
),
��![]() =(x2-x1,y2-y1),
=(x2-x1,y2-y1),
��![]() =p(x2-x1)
=p(x2-x1)![]()
=p(x2-x1)![]() =0.
=0.
��![]() .
.
���PDB�ա�PBF.
���BPF=��DPB=��.
���+2��=90��=��+��.���=��-��.
����kAB��0,��Ƣڿ��C��=��-��,
���=|��-��|.



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
| 1 |
| 3 |
| a-3 |
| 2 |
| x | 2 1 |
| x | 2 2 |
| x | 3 1 |
| x | 3 2 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
| x |
| 1+x |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 2 |
| 19 |
| 2 |
| 19 |
| 2 |
| 1 |
| 2 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| x |
| ||
1+
|
| x |
| 1+x |
| 1 |
| 1+x |
| x |
| 1+x |
| 1+x |
| 1+x |
| 1 | ||
2x+
|
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
| ||
| 1-x |
| 1 |
| 2 |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| lim |
| n���� |
| 4Sn-9Sn |
| 4Sn+1+9Sn+1 |
|
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
| x+1-a |
| a-x |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
| ||
| 1-x |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| sin�� | ||
|
�鿴�𰸺ͽ���>>
���H�WУ��(y��u)�x - �������б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com