
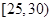 ,第2組
,第2組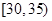 ,第3組
,第3組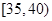 ,第4組
,第4組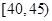 ,第5組
,第5組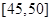 ,由統計的數據得到的頻率分布直方圖如圖所示,在其右面的表是年齡的頻率分布表。
,由統計的數據得到的頻率分布直方圖如圖所示,在其右面的表是年齡的頻率分布表。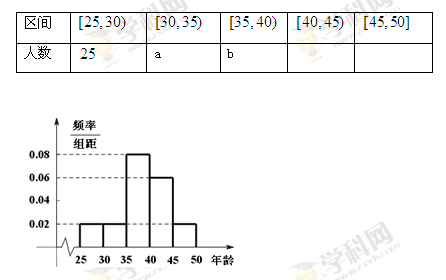
科目:高中數學 來源:不詳 題型:解答題
 名高三學生,得到如圖所示的頻率分布直方圖.
名高三學生,得到如圖所示的頻率分布直方圖. 的值;
的值; 的學生中隨機選取
的學生中隨機選取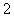 人,求這2人視力均在
人,求這2人視力均在 的概率
的概率
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 產品編號 | A1 | A2 | A3 | A4 | A5 |
| 質量指標(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| 產品編號 | A6 | A7 | A8 | A9 | A10 |
| 質量指標(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
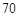 分的學生數是 .
分的學生數是 .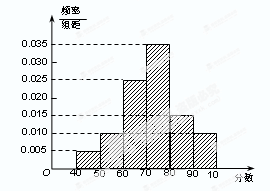
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
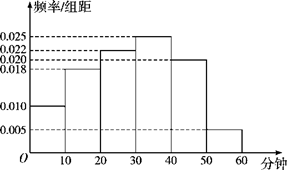
| | 非積極分子 | 積極分子 | 合計 |
| 男 | | 15 | 45 |
| 女 | | | |
| 合計 | | | |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
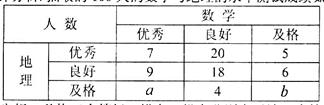
 ,求在地理成績及格的學生中,數學成績優秀的人數比及格的人數少的概率.
,求在地理成績及格的學生中,數學成績優秀的人數比及格的人數少的概率.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| x | 0 | 1 | 2 | 3 |
| y | 0 | 2 | 6 | 7 |
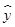 =
= x+
x+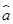 必過點( )
必過點( )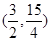 D.(3,7)
D.(3,7)查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 的分布列與期望.
的分布列與期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com