Question

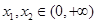設函數，對任意，不等式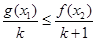恒成立，則正數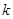的取值范圍是       

Answer 1

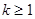
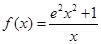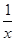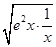解析試題分析：因為，當x＞0時，=e²x+≥2=2e
所以x₁∈（0，+∞）時，函數f（x₁）有最小值2e
因為，g(x)=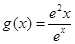，所以，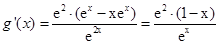
當x＜1時，g′（x）＞0，則函數g（x）在（0，1）上單調遞增
當x＞1時，g′（x）＜0，則函數在（1，+∞）上單調遞減
∴x=1時，函數g（x）有最大值g（1）=e
則有x₁、x₂∈（0，+∞），f（x₁）_min=2e＞g（x₂）_max=e
又因為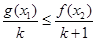，恒成立且k＞0
所以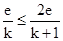，，所以，k≥1，故答案為k≥1。
考點：本題主要考查利用導數研究函數的單調性，均值定理的應用。
點評：中檔題，解答本題的關鍵是認識到，由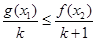恒成立且k＞0，
確定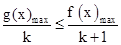，將問題轉化成求函數的最值問題。本題難度較大。