
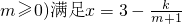 )(k為常數)滿足:x=3-
)(k為常數)滿足:x=3-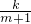 ,如果不搞促銷活動,則該產品的年銷售量只能是1萬件.已知2004年生產該產品的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元,廠家將每件產品的銷售價格定為每件產品年平均成本的1.5倍(產品成本包括固定投入和再投入兩部分資金).
,如果不搞促銷活動,則該產品的年銷售量只能是1萬件.已知2004年生產該產品的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元,廠家將每件產品的銷售價格定為每件產品年平均成本的1.5倍(產品成本包括固定投入和再投入兩部分資金). ;
;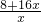 (萬元),
(萬元),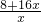 ]-(8+16x+m)
]-(8+16x+m)  )-m
)-m +(m+1)]+29(m≥0).
+(m+1)]+29(m≥0). +(m+1)]+29(m≥0),
+(m+1)]+29(m≥0), +(m+1)≥2
+(m+1)≥2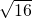 =8,
=8, =m+1,即m=3(萬元)時,ymax=21(萬元).
=m+1,即m=3(萬元)時,ymax=21(萬元).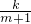 ,當m=0時,x=1,可得k的值,即得x關于m的解析式;又每件產品的銷售價格為1.5×
,當m=0時,x=1,可得k的值,即得x關于m的解析式;又每件產品的銷售價格為1.5×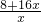 (萬元),則利潤y=x[1.5×
(萬元),則利潤y=x[1.5×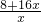 ]-(8+16x+m)整理即可.(2)對(1)利潤函數y=-[
]-(8+16x+m)整理即可.(2)對(1)利潤函數y=-[ +(m+1)]+29(m≥0),利用基本不等式求最大值即可.
+(m+1)]+29(m≥0),利用基本不等式求最大值即可. (a>0,b>0)的靈活運用,是中檔題目.
(a>0,b>0)的靈活運用,是中檔題目. 

科目:高中數學 來源: 題型:
| 2 | m+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| k |
| m+1 |
| k |
| m+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 | x+1 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| k |
| m+1 |
| k |
| m+1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com