
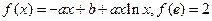 (e=2.71828…是自然對數的底數).
(e=2.71828…是自然對數的底數).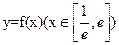 都有公共點?若存在,求出最小的實數m和最大的實數M;若不存在,說明理由.
都有公共點?若存在,求出最小的實數m和最大的實數M;若不存在,說明理由. 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
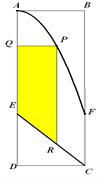
 企
企 業擬建造如圖所示的容器(不計厚度,長度單位:米),其中容器的中間為圓柱形,左右兩端均為半球形,按照設計要求容器的體積為
業擬建造如圖所示的容器(不計厚度,長度單位:米),其中容器的中間為圓柱形,左右兩端均為半球形,按照設計要求容器的體積為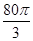 立方米,且
立方米,且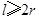 .假設該容器的建造費用僅與其表面積有關.已知圓柱形部分每平方米建造費用為3千元,半球形部分每平方米建造費用為
.假設該容器的建造費用僅與其表面積有關.已知圓柱形部分每平方米建造費用為3千元,半球形部分每平方米建造費用為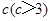 .設該容器的建造費用為
.設該容器的建造費用為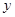 千元.
千元.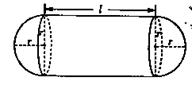
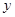
 關于
關于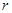 的函數表達式,并求該函數的定義域;
的函數表達式,并求該函數的定義域;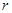 .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
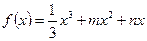 .
.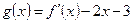 在
在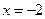 處取得最小值
處取得最小值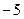 ,求
,求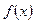 的解析式;
的解析式; ,
,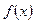 的單調遞減區間的長度是正整數,試求
的單調遞減區間的長度是正整數,試求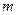 和
和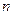
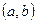 的長度為
的長度為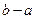 )
)查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com