
函數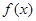 是定義在
是定義在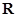 上的偶函數,且對任意的
上的偶函數,且對任意的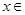
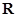 ,都有
,都有 .當
.當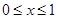 時,
時,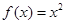 .若直線
.若直線 與函數
與函數 的圖象有兩個不同的公共點,則實數
的圖象有兩個不同的公共點,則實數 的值為( )
的值為( )
A.
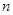
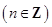 B.
B.
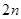
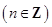
C.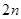 或
或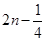
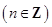 D.
D.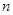 或
或
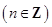
C
【解析】
試題分析:解:因為函數f(x)是定義在R上的偶函數,設x∈[-1,0],則-x∈[0,1],于是f(x)=(-x)2=x2.
設x∈[1,2],則(x-2)∈[-1,0].于是,f(x)=f(x-2)=(x-2)2.
①當a=0時,聯立y="x," y=x2,解得x=0,y=0,或x=y=1,即當a=0時,即直線y=x+a與函數y=f(x)的圖象有兩個不同的公共點.
②當-2<a<0時,只有當直線y=x+a與函數f(x)=x2在區間[0,1)上相切,且與函數f(x)=(x-2)2在x∈[1,2)上僅有一個交點時才滿足條件.由f′(x)=2x=1,解得x=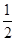 ∴y=(
∴y=(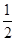 )2=
)2=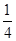 ,故其切點為(
,故其切點為(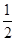 ,
,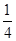 )
)
),∴a=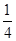 -
-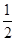 =-
=-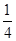 由y=x-
由y=x-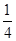 , y=(x-2)2(1≤x<2)解之得x=
, y=(x-2)2(1≤x<2)解之得x= 綜上①②可知:直線y=x+a與函數y=f(x)在區間[0,2)上的圖象有兩個不同的公共點時的a的值為0或-
綜上①②可知:直線y=x+a與函數y=f(x)在區間[0,2)上的圖象有兩個不同的公共點時的a的值為0或-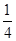 又函數f(x)是定義在R上的偶函數,且對任意的x∈R,都有f(x+2)=f(x),實數a的值為
又函數f(x)是定義在R上的偶函數,且對任意的x∈R,都有f(x+2)=f(x),實數a的值為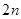 或
或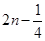 ,(n∈Z).故應選C.
,(n∈Z).故應選C.
考點:函數的奇偶性、周期性
點評:此題考查了函數的奇偶性、周期性及導數的應用,用到了數形結合的思想方法


科目:高中數學 來源: 題型:單選題
查看答案和解析>>
科目:高中數學 來源: 題型:
已知![]() 是定義在
是定義在![]() 上的不恒為零的函數,且對于任意實數
上的不恒為零的函數,且對于任意實數![]() 都有
都有![]() , 則
, 則
(A)![]() 是奇函數,但不是偶函數 (B)
是奇函數,但不是偶函數 (B)![]() 是偶函數,但不是奇函數
是偶函數,但不是奇函數
(C)![]() 既是奇函數,又是偶函數 (D)
既是奇函數,又是偶函數 (D)![]() 既非奇函數,又非偶函
既非奇函數,又非偶函
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com