
已知橢圓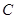 方程為
方程為 ,左、右焦點分別是
,左、右焦點分別是 ,若橢圓
,若橢圓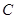 上的點
上的點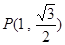 到
到 的距離和等于
的距離和等于 .
.
(Ⅰ)寫出橢圓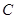 的方程和焦點坐標;
的方程和焦點坐標;
(Ⅱ)設點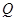 是橢圓
是橢圓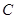 的動點,求線段
的動點,求線段 中點
中點 的軌跡方程;
的軌跡方程;
(Ⅲ)直線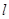 過定點
過定點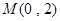 ,且與橢圓
,且與橢圓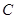 交于不同的兩點
交于不同的兩點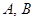 ,若
,若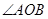 為銳角(
為銳角(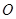 為坐標原點),求直線
為坐標原點),求直線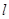 的斜率
的斜率 的取值范圍.
的取值范圍.
(Ⅰ)橢圓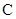 的方程
的方程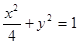 ,焦點
,焦點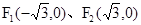
(Ⅱ)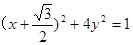 (Ⅲ)
(Ⅲ)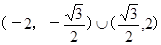
【解析】
試題分析:(Ⅰ)由題意得: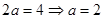 ,
,
又點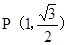 橢圓
橢圓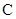 上,∴
上,∴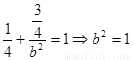
∴ 橢圓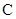 的方程
的方程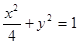 ,焦點
,焦點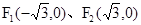 . ……5分
. ……5分
(Ⅱ)設橢圓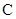 上的動點
上的動點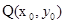 ,線段
,線段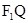 中點
中點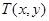 ,
,
由題意得: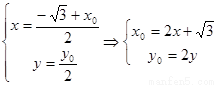 ,
,
代入橢圓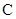 的方程得,
的方程得, ,
,
即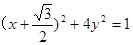 為線段
為線段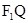 中點
中點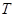 的軌跡方程. ……9分
的軌跡方程. ……9分
(Ⅲ)由題意得直線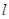 的斜率存在且不為
的斜率存在且不為 ,
,
設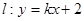 代入
代入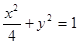 整理,
整理,
得 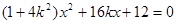 ,
,
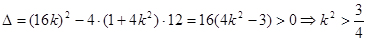 ①
①
設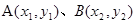 ,∴
,∴ 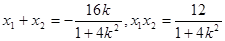
∵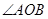 為銳角
為銳角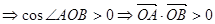 ,即
,即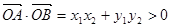 ,
,
又 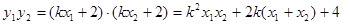 .
.
∴ 
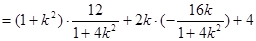
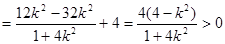 , ∴
, ∴ 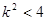 . ②
. ②
由①、②得 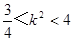 ,∴
,∴ 的取值范圍是
的取值范圍是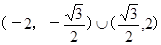 . ……14分
. ……14分
考點:本小題注意考查橢圓標準方程的求解,直線與橢圓的位置關系等.
點評:圓錐曲線的綜合問題一般離不開直線方程和圓錐曲線方程聯立方程組,運算量較大,注意到聯立得到直線方程后,不要忘記驗證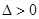 .
.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:高中數學 來源: 題型:
| x2 |
| 2 |
| EG |
| F2E |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年四川省成都市高新區高三2月月考理科數學試卷(解析版 題型:填空題
已知橢圓方程為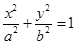 (
(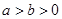 ),F
),F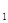 (-c,0)和F
(-c,0)和F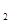 (c,0)分別是橢圓的左 右焦點.
(c,0)分別是橢圓的左 右焦點.
①若P是橢圓上的動點,延長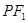 到M,使
到M,使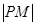 =
=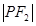 ,則M的軌跡是圓;
,則M的軌跡是圓;
②若P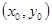 是橢圓上的動點,則
是橢圓上的動點,則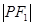
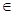
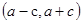 ;
;
③以焦點半徑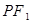 為直徑的圓必與以長軸為直徑的圓內切;
為直徑的圓必與以長軸為直徑的圓內切;
④若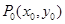 在橢圓
在橢圓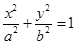 上,則過
上,則過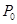 的橢圓的切線方程是
的橢圓的切線方程是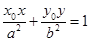 ;
;
⑤點P為橢圓上任意一點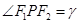 ,則橢圓的焦點角形的面積為
,則橢圓的焦點角形的面積為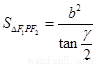 .
.
以上說法中,正確的有
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2012-2013學年上海市閔行區七寶中學高三(下)摸底數學試卷(解析版) 題型:解答題
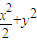 =1,它的左、右焦點分別為F1、F2.點P(x,y)為第一象限內的點.直線PF1和PF2與橢圓的交點分別為A、B和C、D,O為坐標原點.
=1,它的左、右焦點分別為F1、F2.點P(x,y)為第一象限內的點.直線PF1和PF2與橢圓的交點分別為A、B和C、D,O為坐標原點.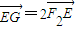 ,求p的最大值.
,求p的最大值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com