Question

已知正方形ABCD的邊長為1，記以A為起點，其余頂點為終點的向量分別為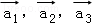；以C為起點，其余頂點為終點的向量分別為，若i，j，k，l∈{1，2，3}，且i≠j，k≠l，則的最小值是　 　．

Answer 1

﹣5

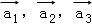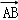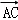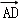解析試題分析：不妨記以A為起點，其余頂點為終點的向量分別為，，，以C為起點，其余頂點為終點的向量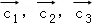分別為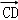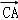，，．如圖建立坐標系．
（1）當i=1，j=2，k=1，l=2時，則=[（1，0）+（1，1）]•[（（﹣1，0）+（﹣1，﹣1）]=﹣5；
（2）當i=1，j=2，k=1，l=3時，則=[（1，0）+（1，1）]•[（（﹣1，0）+（0，﹣1）]=﹣3；
（3）當i=1，j=2，k=2，l=3時，則=[（1，0）+（1，1）]•[（（﹣1，﹣1）+（0，﹣1）]=﹣4；
（4）當i=1，j=3，k=1，l=2時，則=[（1，0）+（0，1）]•[（（﹣1，0）+（﹣1，﹣1）]=﹣3；
同樣地，當i，j，k，l取其它值時，=﹣5，﹣4，或﹣3．
則的最小值是﹣5．
故答案為：﹣5．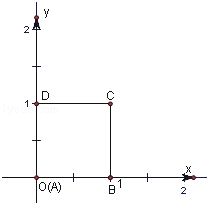

考點：平面向量數量積的運算
點評：本小題主要考查平面向量坐標表示、平面向量數量積的運算等基本知識，考查考查分類討論、化歸以及數形結合等數學思想方法，考查分析問題、解決問題的能力