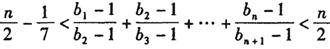(14分)
已知數(shù)列
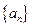
的前
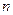
項和為
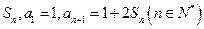
(1)求
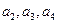
的值;
(2)求數(shù)列
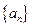
的通項公式;
(3)設(shè)
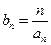
,求證:數(shù)列
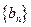
的前
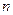
項和
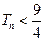
。
解(1)由已知,得
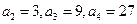
………………………………(3分)
(2)由
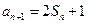
…………………①
得,當
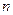
≥2時,
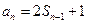
……②
①-②,得
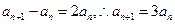
(
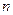
≥2)………

…………(5分)
又
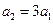
……………………………………………………………………(6分)
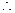
數(shù)列
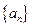
是等比數(shù)列,首項
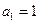
,公比
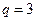
。
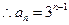
………(8分

)
(3)由

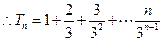
…………③
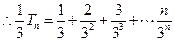
………④ …………………………(9分)
③-④,得
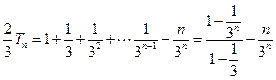
…………(11分)
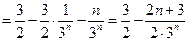
……………………(12分

)

練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:填空題
在等差數(shù)列
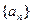
中,若
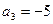
,
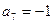
,則
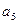
的值為____▲______。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
記
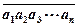
為一個
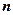
位正整數(shù),其中
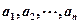
都是正整數(shù),

.若對任意的正整數(shù)
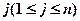
,

至少存在另一個正整數(shù)
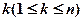
,使得
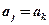
,則稱這個數(shù)為“
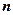
位重復(fù)數(shù)”.根據(jù)上述定義,“四位重復(fù)數(shù)”的個數(shù)為.____________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知
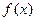
是定義在
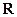
上不恒為零的函數(shù),對于任意的
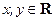
,都有
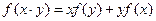
成立.數(shù)列
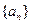
滿足
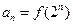
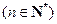
,且
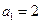
.則數(shù)列的通項公式
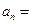
_____ .
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
、如果等差數(shù)列
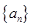
中,
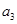
+
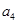
+
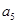
=12,那么
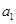
+

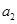
+…+
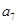
=( )
| A.21 | B.28 | C. 14 14 | D.35 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
.如果等差數(shù)列
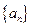
中,
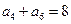
,那么數(shù)列
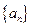
的前9項和

為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分14分)
已知數(shù)列
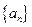
滿足
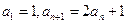
,
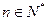
.
(1)求數(shù)列
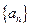
的通項公式;
(2)設(shè)
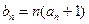
,求數(shù)列
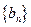
的前
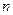
項和
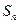
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知數(shù)列
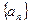
為等差數(shù)列,
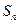
是它的前

項和.若
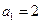
,
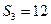
,則
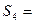
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分14分)
已知數(shù)列
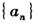
的前n項和
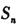
滿足
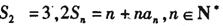
.
(2) 求
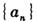
的通項公式,并求數(shù)列
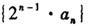
的前n項和
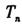
;
(3) 設(shè)
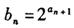
,證明:
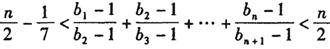
查看答案和解析>>

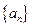 的前
的前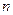 項和為
項和為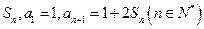
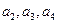 的值;
的值; 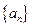 的通項公式;
的通項公式; 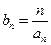 ,求證:數(shù)列
,求證:數(shù)列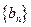 的前
的前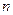 項和
項和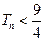 。
。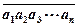 為一個
為一個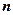 位正整數(shù),其中
位正整數(shù),其中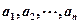 都是正整數(shù),
都是正整數(shù), .若對任意的正整數(shù)
.若對任意的正整數(shù)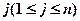 ,
, 至少存在另一個正整數(shù)
至少存在另一個正整數(shù)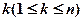 ,使得
,使得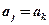 ,則稱這個數(shù)為“
,則稱這個數(shù)為“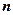 位重復(fù)數(shù)”.根據(jù)上述定義,“四位重復(fù)數(shù)”的個數(shù)為.____________.
位重復(fù)數(shù)”.根據(jù)上述定義,“四位重復(fù)數(shù)”的個數(shù)為.____________. 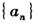 的前n項和
的前n項和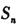 滿足
滿足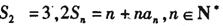 .
.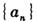 的通項公式,并求數(shù)列
的通項公式,并求數(shù)列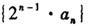 的前n項和
的前n項和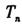 ;
;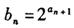 ,證明:
,證明: