中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

如圖，直線l與拋物線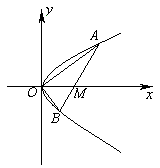交于兩點，與x軸相交于點M，且．

(1)求證：M點的坐標為(1，0)；

(2)求證：OA⊥OB；

(3)求△AOB的面積的最小值．

答案：
解析：

答案：(3)1

(1 ) 設M點的坐標為(x0，0)，直線l方程為 x =my + x0 ，代入y2 =x得

y2－my－x0 =0　　　　①　　y1、y2是此方程的兩根，

∴ x0 ＝－y1y2 ＝1，即M點的坐標為(1，0)．

(2 ) ∵ y1y2 ＝－1

∴ x1x2 + y1y2 =y12y22 +y1y2 ＝y1y2 (y1y2 +1) =0

∴　OA⊥OB．

(3)由方程①，y1＋y2 =m ，　y1y2 ＝－1 ，　且 | OM | =x0 =1，

于是S△AOB =| OM | |y1－y2| ==≥1，

∴ 當m =0時，△AOB的面積取最小值1．


練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

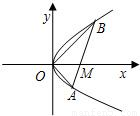
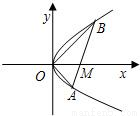
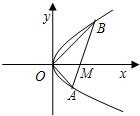精英家教網如圖，直線l與拋物線y2=x交于A（x1，y1），B（x2，y2）兩點，與x軸相交于點M，且y1y2=-1．
（1）求證：M點的坐標為（1，0）；
（2）求證：OA⊥OB；
（3）求△AOB的面積的最小值．

查看答案和解析>>

科目：高中數學 來源：0103 月考題 題型：解答題

如圖，直線l與拋物線y2=x交于A（x1，y1），B（x2，y2）兩點，與x軸相交于點M，且y1y2=-1，
（1）求證：M點的坐標為（1，0）；
（2）求證：OA⊥OB；
（3）求△AOB的面積的最小值。

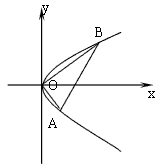
查看答案和解析>>

科目：高中數學 來源：不詳 題型：解答題

如圖，直線l與拋物線y2=x交于A（x1，y1），B（x2，y2）兩點，與x軸相交于點M，且y1y2=-1．
（1）求證：M點的坐標為（1，0）；
（2）求證：OA⊥OB；
（3）求△AOB的面積的最小值．
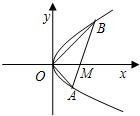
精英家教網

查看答案和解析>>

科目：高中數學 來源：2012-2013學年河南省駐馬店市泌陽一高高二（上）12月月考數學試卷（文科）（解析版） 題型：解答題

如圖，直線l與拋物線y2=x交于A（x1，y1），B（x2，y2）兩點，與x軸相交于點M，且y1y2=-1．
（1）求證：M點的坐標為（1，0）；
（2）求證：OA⊥OB；
（3）求△AOB的面積的最小值．

查看答案和解析>>

科目：高中數學 來源：2011年高三數學單元檢測：圓錐曲線與方程（2）（解析版） 題型：解答題

如圖，直線l與拋物線y2=x交于A（x1，y1），B（x2，y2）兩點，與x軸相交于點M，且y1y2=-1．
（1）求證：M點的坐標為（1，0）；
（2）求證：OA⊥OB；
（3）求△AOB的面積的最小值．

查看答案和解析>>

同步練習冊答案