
已知雙曲線C的方程為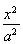 -
-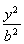 =1(a>0,b>0),離心率e=
=1(a>0,b>0),離心率e=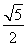 ,頂點到漸近線的距離為
,頂點到漸近線的距離為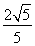 .
.

(1)求雙曲線C的方程;
(2)如圖,P是雙曲線C上一點,A、B兩點在雙曲線C的兩條漸近線上,且分別位于第一、二象限.若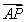 =λ
=λ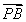 ,λ∈
,λ∈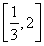 .求△AOB的面積的取值范圍.
.求△AOB的面積的取值范圍.
(1)  -x2=1 (2)
-x2=1 (2) 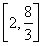
【解析】
解:(1)由題意知,雙曲線C的頂點(0,a)到漸近線ax-by=0的距離為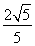 ,
,
∴ =
=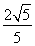 ,即
,即 =
=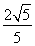 .
.
由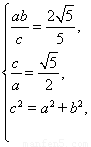 得
得
∴雙曲線C的方程為 -x2=1.
-x2=1.
(2)由(1)知雙曲線C的兩條漸近線方程為y=±2x,
設A(m,2m),B(-n,2n),m>0,n>0.
由 =λ
=λ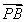 得P點坐標為
得P點坐標為 ,
,
將P點坐標代入 -x2=1,化簡得mn=
-x2=1,化簡得mn= .
.
設∠AOB=2θ,∵tan( -θ)2.
-θ)2.
∴tanθ= ,sin2θ=
,sin2θ=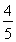 .
.
又|OA|=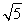 m,|OB|=
m,|OB|=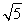 n,
n,
∴S△AOB= |OA|·|OB|·sin2θ
|OA|·|OB|·sin2θ
=2mn
=
 +1,
+1,
記S(λ)=
 +1,λ∈
+1,λ∈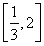 .
.
則S′(λ)=
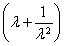 .
.
由S′(λ)=0得λ=1.
又S(1)=2,S =
=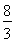 ,S(2)=
,S(2)= ,
,
∴當λ=1時,△AOB的面積取得最小值2,當λ= 時,
時,
△AOB的面積取得最大值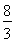 .
.
∴△AOB面積的取值范圍是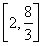 .
.


科目:高中數學 來源: 題型:
| y2 |
| 4 |
| AP |
| PB |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com