
(Ⅰ)求A1B與平面ABD所成角的大小(結果用反三角函數值表示);
(Ⅱ)求點A1到平面AED的距離.
18.

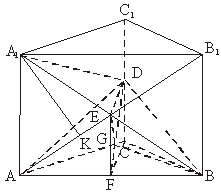
(Ⅰ)解:連結BG,則BG是BE在面ABD的射影,即∠EBG是A1B與平面ABD所成的角.
設F為AB中點,連結EF、FC,
∵D、E分別是CC1、A1B的中點,又DC⊥平面ABG,
∴CDEF為矩形.
連結DF,G是△ADB的重心,∴G![]() DF.
DF.
在直角三角形EFD中,EF2=FG·FD=![]() FD2,
FD2,
∵EF=1∴FD=![]() .于是ED=
.于是ED=![]() ,EG=
,EG=![]() =
=![]() ,
,
∵FG=ED=![]() ,∴AB=2
,∴AB=2![]() ,A1B=2
,A1B=2![]() ,EB=
,EB=![]() ,
,
∴sinEBG=![]() =
=![]() ·
·![]() =
=![]() ,
,
∴A1B與平面ABD所成的角是arcsin![]() .
.
(Ⅱ)解法一:∵ED⊥AB,ED⊥EF,又EF∩AB=F,
∴ED⊥面A1AB,
又ED![]() 面AED,
面AED,
∴平面AED⊥平面A1AB,且面AED∩面A1AB=AE.
作A1K⊥AE,垂足為K,
∴A1K⊥平面AED.即A1K是A1到平面AED的距離.
在△A1AB1中,A1K=![]() =
=![]() =
=![]() ,
,
∴A1到平面AED的距離為![]() .
.
解法二:連結A1D,有![]() =
=![]() .
.
∵ED⊥AB,ED⊥EF,又EF∩AB=F,
∴ED⊥平面A1AB,
設A1到平面AED的距離為h,
則 ![]() ·h=
·h=![]() ·ED.
·ED.
又![]() =
=![]()
![]() =
=![]() A
A![]() ,
,
![]() =
=![]() AE·ED=
AE·ED=![]() .
.
∴h=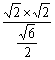 =
=![]() .
.
即A1到平面AED的距離為![]() .
.


科目:高中數學 來源: 題型:
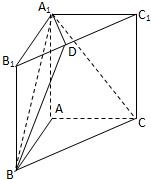 如圖,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=a,AC=2,AA1=1,點D在棱B1C1上且B1D:DC1=1:3
如圖,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=a,AC=2,AA1=1,點D在棱B1C1上且B1D:DC1=1:3查看答案和解析>>
科目:高中數學 來源: 題型:
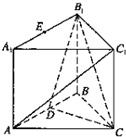 如圖,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,D是AB的中點.
如圖,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,D是AB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:
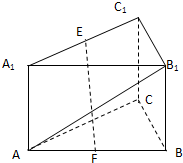 如圖,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=a,E是A1C1的中點,F是AB中點.
如圖,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=a,E是A1C1的中點,F是AB中點.查看答案和解析>>
科目:高中數學 來源: 題型:
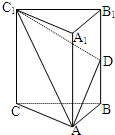 如圖,在直三棱柱ABC-A1B1C1中,A1A=AC=
如圖,在直三棱柱ABC-A1B1C1中,A1A=AC=| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com