
設函數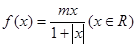 ,區間
,區間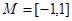 ,集合
,集合 ,則使
,則使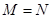 成立的實數
成立的實數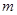 的個數為
的個數為
A.1 B.2 C.3 D.無數
B
【解析】
試題分析:先判斷函數f(x)是奇函數,題意可得,當-1≤x≤1時,函數的值域為[-1,1].分m>0和m<0 兩種情況,分別利用函數的單調性求得m的值,綜合可得結論。根據題意,函數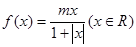 ,可得
,可得
 ,故為奇函數,同時
,故為奇函數,同時
題意可得,當-1≤x≤1時,函數的值域為[-1,1].①若x∈[0,1],且m>0,
故函數在[0,1]上是增函數,故函數f(x)在區間M=[-1,1]上是增函數,故有f(-1)=-1,f(1)=1,即
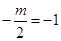 ,解得 m=2.
,解得 m=2.
②若x∈[0,1],且m<0,由 f(x)= ,故函數在[0,1]上是減函數,故函數f(x)在區間M=[-1,1]上是減函數,故有f(-1)=1,f(1)=-1,即
,故函數在[0,1]上是減函數,故函數f(x)在區間M=[-1,1]上是減函數,故有f(-1)=1,f(1)=-1,即 解得 m=-2.
解得 m=-2.
③顯然,m=0不滿足條件.
綜上可得,m=±2,故使M=N成立的實數m的個數為2,
故選B.
考點:函數奇偶性以及參數范圍
點評:本題主要考查集合關系中參數的取值范圍問題,函數的奇偶性、單調性的應用,體現了分類討論的數學思想,屬于基礎題.


科目:高中數學 來源:2015屆重慶第十八中學高一上10月月考數學試卷(解析版) 題型:選擇題
設函數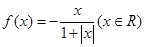 ,區間
,區間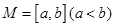 ,集合
,集合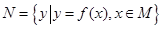 ,則使M=N成立的實數對
,則使M=N成立的實數對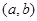 有( )
有( )
A.0個 B.1個 C.2個 D.無數多個
查看答案和解析>>
科目:高中數學 來源:2010-2011學年吉林省高三上學期第二次摸底考試理科數學卷 題型:選擇題
設函數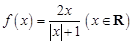 ,區間
,區間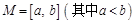 ,集合
,集合
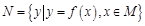 ,則使
,則使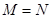 成立的實數對
成立的實數對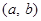 有 ( )
有 ( )
A.0對 B. 1對 C.2對 D.3對
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com